To tylko jedna z 5 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
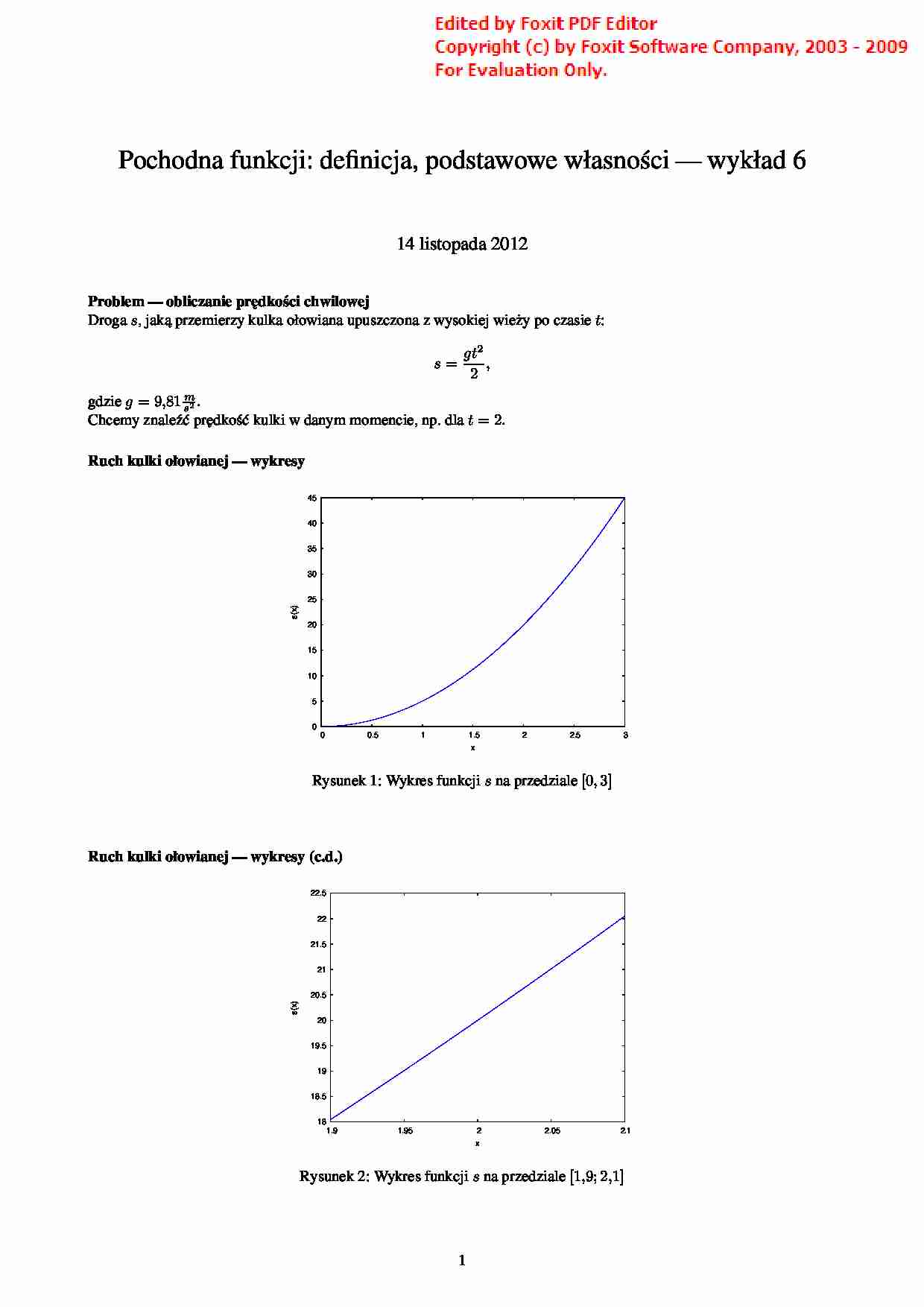


Pochodna funkcji: definicja, podstawowe własno´sci — wykład 6 14 listopada 2012 Problem — obliczanie pr˛edko´sci chwilowej Droga s , jak ˛ a przemierzy kulka ołowiana upuszczona z wysokiej wie˙zy po czasie t : s = gt 2 2 , gdzie g = 9 , 81 m s 2 . Chcemy znale´z´c pr˛edko´s´c kulki w danym momencie, np. dla t = 2 . Ruch kulki ołowianej — wykresy 0 5 10 15 20 25 30 35 40 45 0 0.5 1 1.5 2 2.5 3 s(x) x Rysunek 1: Wykres funkcji s na przedziale [0 , 3] Ruch kulki ołowianej — wykresy (c.d.) 18 18.5 19 19.5 20 20.5 21 21.5 22 22.5 1.9 1.95 2 2.05 2.1 s(x) x Rysunek 2: Wykres funkcji s na przedziale [1 , 9; 2 , 1] 1 19.8 19.85 19.9 19.95 20 20.05 20.1 20.15 20.2 20.25 1.99 1.992 1.994 1.996 1.998 2 2.002 2.004 2.006 2.008 2.01 s(x) x Rysunek 3: Wykres funkcji s na przedziale [1 , 99; 2 , 01] Ruch kulki ołowianej — wykresy (c.d.) Pr˛edko´s´c jako granica funkcji Rozwa˙zmy punkt materialny poruszaj ˛ acy si˛e wzdłu˙z osi OX ; poło˙zenie punktu w chwili t b˛edziemy oznaczali przez S ( t ). Pr˛edko´s´c chwilow ˛ a tego punktu materialnego w chwili t 0 mo˙zna zdefiniowa´c jako: lim t→t 0 S ( t ) − S ( t 0) t − t 0 , je´sli ta granica istnieje. Poj˛ecie granicy funkcji w punkcie Dla dowolnego ci ˛ agu ( dn ) takiego, ˙ze: lim n→∞ dn → 0 , dn = 0 dla n ∈ N , (1) ci ˛ ag v ( dn ) (pr˛edko´sci ´srednich na odcinku [ t, t + dn ]) v ( dn ) = s ( t + dn ) − s ( t ) dn = 0 , 5( gt 2 + 2 gtdn + gd 2 n − gt 2) dn = gt + g dn 2 jest zbie˙zny do granicy wła´sciwej gt . Innymi słowy, gt jest wspóln ˛ a granic ˛ a wszystkich ci ˛ agów v ( dn ) takich, ˙ze ( dn ) spełnia warunki (1). W szczególno´sci: dla t = 2 pr˛edko´s´c chwilowa jest równa 10 · 2 = 20 (jednostka: m s ). Iloraz ró˙znicowy Definicja 1. Niech x 0 ∈ R oraz niech funkcja f bedzie okre´slona przynajmniej na otoczeniu O ( x 0 , r ), gdzie r 0. Ilorazem ró˙znicowym funkcji f w punkcie x 0 odpowiadaj ˛ acym przyrostowi ∆ x , gdzie 0
(…)
… stosowane sa takze symbole
˛ ˙
df
(x0 ), Df (x0 ).
dx
Obliczanie pr˛ dko´ci chwilowej — c.d.
e
s
˙
Pr˛ dko´c ołowianej kulki upuszczonej z wysokiej wiezy w chwili t0 jest równa s (t0 ).
e s´
gt2
Przypominamy: s(t) = 2 .
Mamy:
s(t) − s(t0 )
g
s (t0 ) = lim
= lim (t + t0 ) = gt0 .
t→t0
t→t0 2
t − t0
Obliczanie pochodnej — przykłady
Pochodna w punkcie x0 funkcji liniowej f okre´lonej wzorem f (x) = ax + b…
… funkcji
˛
˛
e
c
˛
˛
f w punkcie x0 b˛ dziemy oznacza´ f+ (x0 ).
e
c
Przykład 1. Dla funkcji f (x) = |x| mamy: f− (0) = −1 i f+ (0) = 1.
Poj˛ cie przedziału w analizie matematycznej
e
Przez przedział b˛ dziemy rozumie´ podzbiór prostej b˛ dacy
e
c
e ˛
• odcinkiem — postaci [a, b], [a, b), (a, b] lub (a, b);
• półprosta — postaci [a, ∞), (a, ∞), (∞, b] lub (∞, b);
˛
• prosta R.
˛
Uwaga. Przedziałami…
... zobacz całą notatkę






Komentarze użytkowników (0)