To tylko jedna z 6 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
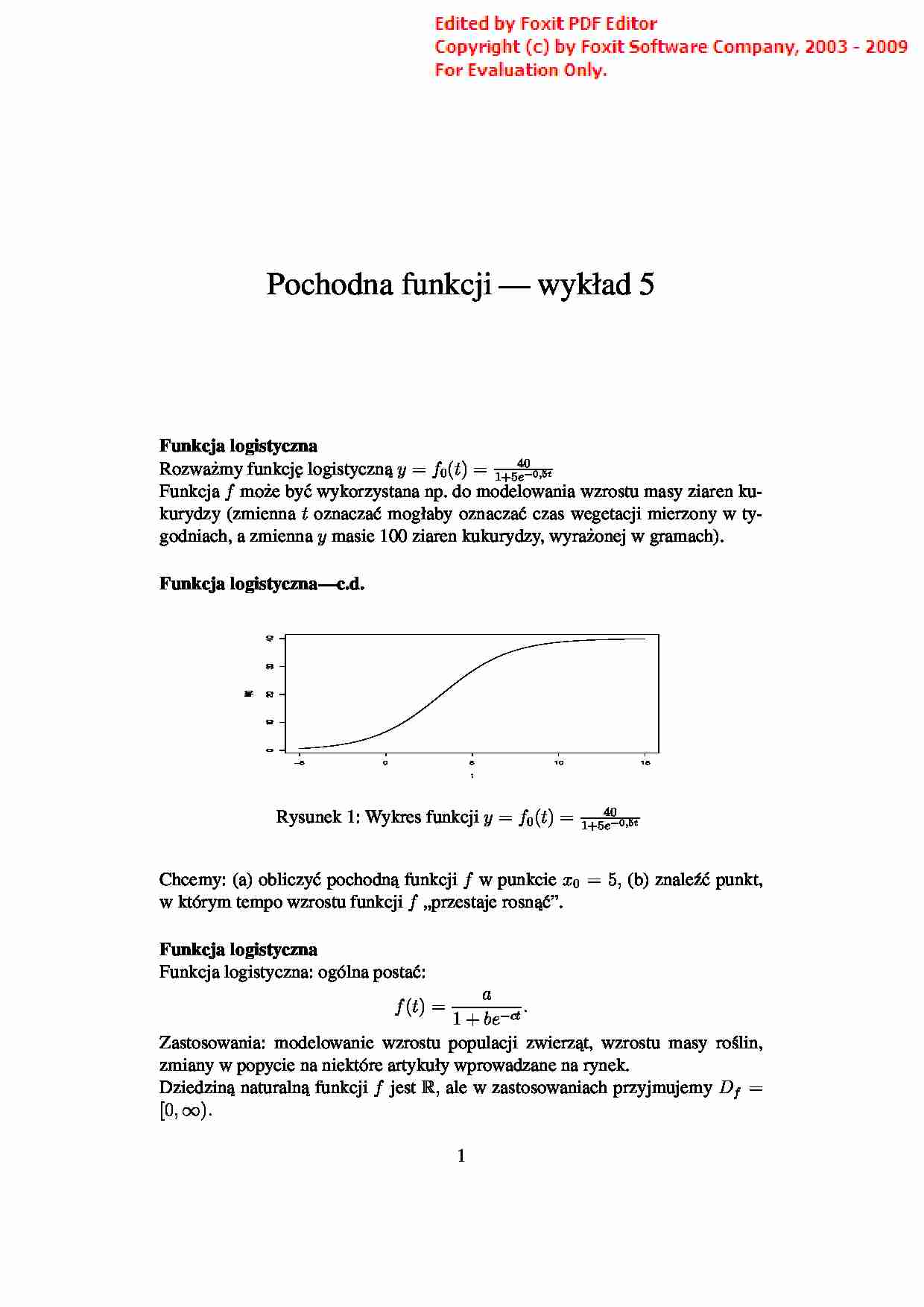


Pochodna funkcji — wykład 5 Funkcja logistyczna Rozwa˙zmy funkcj˛e logistyczn ˛ a y = f 0( t ) = 40 1+5 e− 0 , 5 t Funkcja f mo˙ze by´c wykorzystana np. do modelowania wzrostu masy ziaren ku- kurydzy (zmienna t oznacza´c mogłaby oznacza´c czas wegetacji mierzony w ty- godniach, a zmienna y masie 100 ziaren kukurydzy, wyra˙zonej w gramach). Funkcja logistyczna—c.d. −5 0 5 10 15 0 10 20 30 40 t f(t) Rysunek 1: Wykres funkcji y = f 0( t ) = 40 1+5 e− 0 , 5 t Chcemy: (a) obliczy´c pochodn ˛ a funkcji f w punkcie x 0 = 5 , (b) znale´z´c punkt, w którym tempo wzrostu funkcji f „przestaje rosn ˛ a´c”. Funkcja logistyczna Funkcja logistyczna: ogólna posta´c: f ( t ) = a 1 + be−ct . Zastosowania: modelowanie wzrostu populacji zwierz ˛ at, wzrostu masy ro´slin, zmiany w popycie na niektóre artykuły wprowadzane na rynek. Dziedzin ˛ a naturaln ˛ a funkcji f jest R , ale w zastosowaniach przyjmujemy Df = [0 , ∞ ) . 1 Pr˛edko´s´c wzrostu w chwili t 0— warto´s´c przybli˙zona Chc ˛ ac znale´z´c warto´s´c przybli˙zon ˛ a pr˛edko´sci wzrostu funkcji f 0 w chwili t 0 = 5 mo˙zna obliczy´c iloraz f 0(5 + ∆ x ) ∆ x , (1) gdzie ∆ x jest równa np. 0 , 01 lub 0 , 001 . Mo˙zna sprawdzi´c, ˙ze wyra˙zenie (1) dla ∆ x = 0 , 01 jest równe 4 , 122012 a dla ∆ x = 0 , 001 jest równe 4 , 125897 . Wyra˙zenie (1), tzw. iloraz ró˙znicowy; jego granica przy ∆ x → 0 : pochodna funkcji f 0 w x 0 = 5 . Iloraz ró˙znicowy Definicja 1. Niech x 0 ∈ R oraz niech funkcja f bedzie okre´slona przynajmniej na otoczeniu O ( x 0 , r ), gdzie r 0. Ilorazem ró˙znicowym funkcji f w punkcie x 0 odpowiadaj ˛ acym przyrostowi ∆ x , gdzie 0
(…)
…
tego zbioru sa równe f (x) nazywamy pochodna funkcji na zbiorze i oznaczamy
˛
˛
przez f .
Poj˛ cie przedziału w analizie matematycznej
e
Przez przedział b˛ dziemy rozumie´ podzbiór prostej b˛ dacy
e
c
e ˛
• odcinkiem — postaci [a, b], [a, b), (a, b] lub (a, b);
• półprosta — postaci [a, ∞), (a, ∞), (∞, b] lub (∞, b);
˛
• prosta R.
˛
5
Pochodna na przedziale nie b˛ dacym zbiorem otwartym
e ˛
Pochodna funkcji…
... zobacz całą notatkę






Komentarze użytkowników (0)