To tylko jedna z 7 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
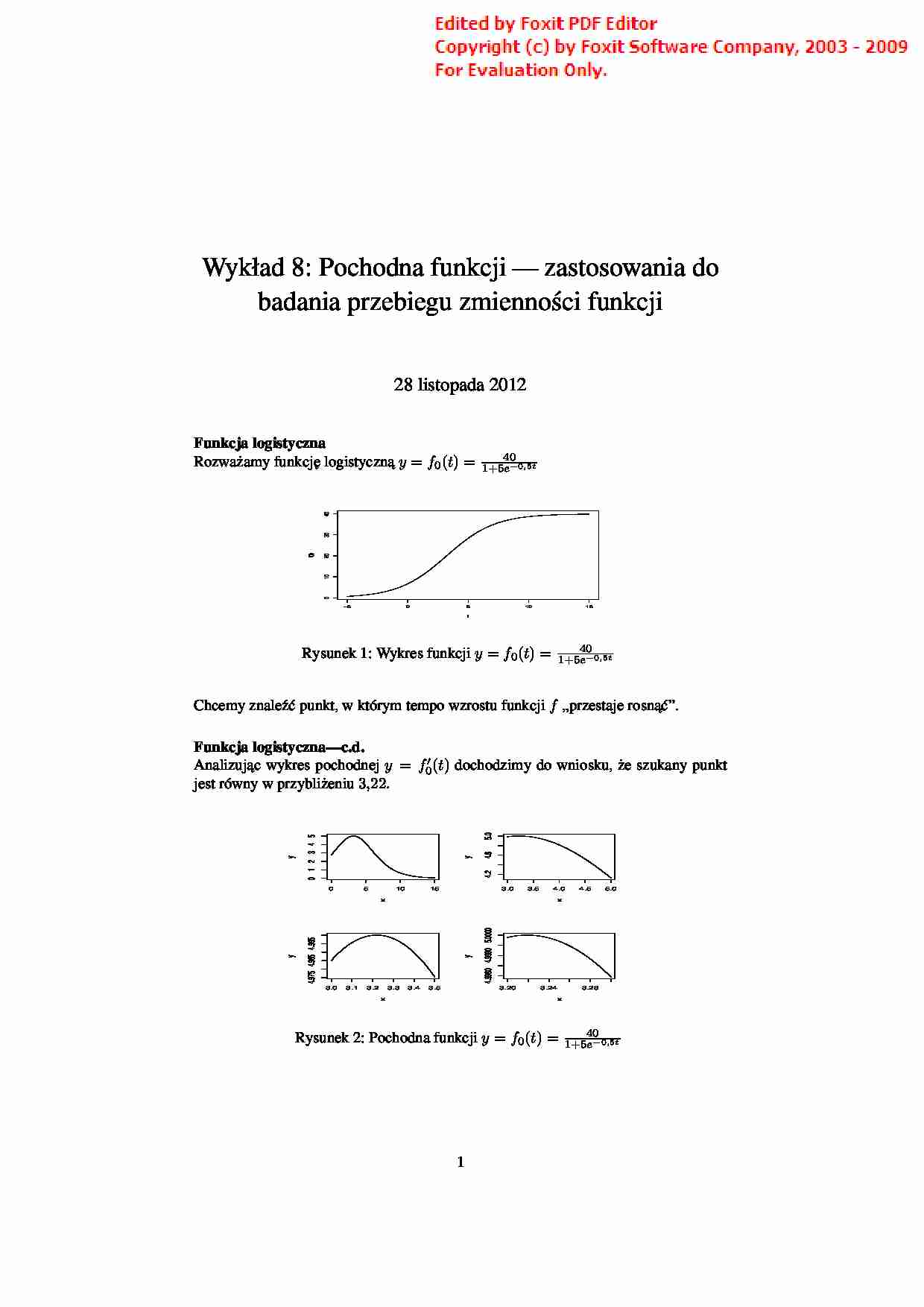


Wykład 8: Pochodna funkcji — zastosowania do badania przebiegu zmienno´sci funkcji 28 listopada 2012 Funkcja logistyczna Rozwa˙zamy funkcj˛e logistyczn ˛ a y = f 0( t ) = 40 1+5 e− 0 , 5 t −5 0 5 10 15 0 10 20 30 40 t f(t) Rysunek 1: Wykres funkcji y = f 0( t ) = 40 1+5 e− 0 , 5 t Chcemy znale´z´c punkt, w którym tempo wzrostu funkcji f „przestaje rosn ˛ a´c”. Funkcja logistyczna—c.d. Analizuj ˛ ac wykres pochodnej y = f 0( t ) dochodzimy do wniosku, ˙ze szukany punkt jest równy w przybli˙zeniu 3 , 22 . 0 5 10 15 0 1 2 3 4 5 x y 3.0 3.5 4.0 4.5 5.0 4.2 4.6 5.0 x y 3.0 3.1 3.2 3.3 3.4 3.5 4.975 4.985 4.995 x y 3.20 3.24 3.28 4.9980 4.9990 5.0000 x y Rysunek 2: Pochodna funkcji y = f 0( t ) = 40 1+5 e− 0 , 5 t 1 Badanie przebiegu funkcji Jest jasne, ˙ze chc ˛ ac znale´z´c szukany punkt nale˙zy zbada´c przebieg zmienno´sci funkcji f 0 . Zaczniemy od przypomnienia definicji poj˛e´c zwi ˛ azanych z badaniem przebiegu funkcji takich jak: minimum lokalne, maksimum lokalne czy druga pochodna. Pochodne wy˙zszych rz˛edów Definicja 1. Mówimy, ˙ze funkcja f jest: • ró˙zniczkowalna w punkcie x 0, je˙zeli ma ona w tym punkcie pochodn ˛ a; • ró˙zniczkowalna na przedziale I , je˙zeli ma pochodn ˛ a w ka˙zdym punkcie tego przedziału. Załó˙zmy, ˙ze funkcja f jest ró˙zniczkowalna na przedziale I . Pochodn ˛ a funkcji f na I (je˙zeli ona istnieje) b˛edziemy oznacza´c przez f (2), (lub f ( )) pochodn ˛ a funkcji f (2) na I (je˙zeli ona istnieje) przez f (3) (lub f ( ) ) itd. Funkcje dwukrotnie ró˙zniczkowalne Definicja 2. Mówimy, ˙ze funkcja f jest: • dwukrotnie ró˙zniczkowalna w punkcie x 0, je˙zeli ma ona w tym punkcie drug ˛ a pochodn ˛ a; • dwukrotnie ró˙zniczkowalna na przedziale I , je˙zeli ma drug ˛ a pochodn ˛ a w ka˙zdym punkcie tego przedziału. Pochodne wy˙zszych rz˛edów— przykłady Dla f ( x ) = x 3 (w tym przypadku obliczamy pochodne na przedziale I = R) mamy: f ( x ) = 3 x 2 , f ( x ) = 6 x, f ( x ) = 6 , f ( n )( x ) = 0 dla n 3 . Pochodne wy˙zszych rz˛edów— przykłady Dla f ( x ) = √ x = x 1 / 2 (w tym przypadku obliczamy pochodne na przedziale I = (0 , ∞ ) mamy: f ( x ) = 1 2 x − 1 / 2 = 1 2 √ x , f ( x ) = 1 2 · ( − 1 / 2) x− 3 / 2 = − 1 4 1 x √ x , itd. 2 Monotoniczno´s´c funkcji na przedziale Załó˙zmy, ˙ze funkcja
(…)
… ˛
f (t) > 0 dla t < t0 ;
f (t) < 0 dla t > t0 ;
f (t) = 0 dla t = t0 .
Ekstremum lokalne— przykład
˙
Rozwazmy funkcj˛
e
1 3 5 2
x − x + 6x.
3
2
˙
Oczywi´cie g jest rózniczkowalna na R. Chcac zbada´ istnienie ekstremów funkcji g
s
˛
c
znajdujemy miejsca zerowe g (x) :
g(x) =
g (x) = x2 − 5x + 6 = 0 ⇔ x = 2 lub x = 3.
4
Mamy:
g (x) > 0 dla x < 2 lub x > 3;
(5)
g (x) < 0 dla x > 2 i x < 3.
(6)
(7)
Stad…
… (x) < 0 dla x ∈ I;
˛
s
• nierosnaca, je´li f (x)
˛
s
0 dla x ∈ I.
Monotoniczno´c funkcji logistycznej
s´
Pochodna funkcji logistycznej
f (t) =
a
.
1 + be−ct
ma posta´
c
f (t) =
abce−ct
.
(1 + be−ct )2
˙
Stad wynika, ze f jest monotoniczna na R.
˛
˙
˙
Monotoniczno´c f mozna tez uzasadni´ , opierajac si˛ na własno´ciach funkcji wykładniczej—
s´
c
˛ e
s
˙
wynika z nich, ze mianownik f jest funkcja malejaca zmiennej x.
˛
˛ ˛
Funkcja logistyczna— c.d.
Druga pochodna f ma posta´ :
c
f (t) =
abc2 e−ct (be−ct − 1)
.
(1 + be−ct )3
Mamy
f (t) = 0 wtedy i tylko wtedy, gdy (be−ct − 1) = 0.
A wi˛ c druga pochodna znika dla t0 = ln b .
e
c
Dla funkcji f0 mamy:
ln b
ln 5
=
≈ 3,218876.
c
0,5
Intuicje geometryczne: znale´ li´my szukany punkt.
z s
Problem: jak uzasadni´ to bardziej formalnie?
c
Ekstremum lokalne…
... zobacz całą notatkę






Komentarze użytkowników (0)