To tylko jedna z 2 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę

optymalna kombinacja czynników produkcji przy danej linii jednakowego nakładu
Załóżmy, że przeciętna płaca pracownika wynosi 1200 jednostek pieniężnych, zaś przeciętna cena maszyn obuwniczych wynosi 1600 jednostek. Ogólny zasób środków finansowych, jakimi dysponuje przedsiębiorstwo, wynosi 96 000 jednostek. Przy nie zmienionej relacji cen czynników wytwórczych przedsiębiorca mógłby nabyć i zastosować za owe 96 000 jednostek pieniężnych następujące kombinacje czynników kapitału i pracy:
liczba maszyn 60 50 40 30 20 10 0 liczba pracowników O 13,3 26,6 40 53,3 66,6 80.
Te kombinacje tworzą linię jednakowego nakładu (lub kosztu). Wszystkie bowiem punkty na tej linii reprezentują możliwe kombinacje nakładów kapitału i pracy, które mogą być nabyte za łączną sumę 96 000 jednostek pieniężnych.
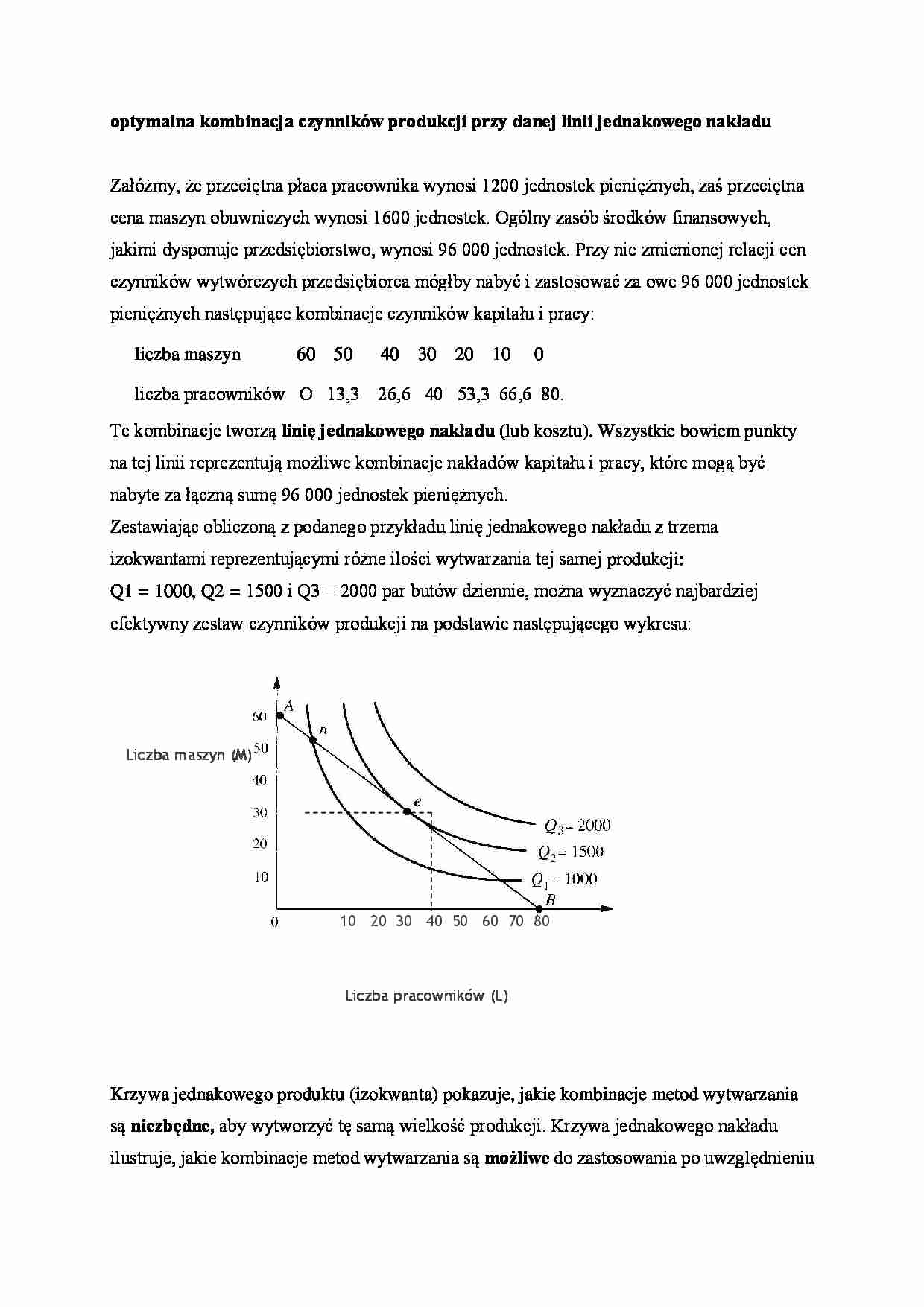
Zestawiając obliczoną z podanego przykładu linię jednakowego nakładu z trzema izokwantami reprezentującymi różne ilości wytwarzania tej samej produkcji: Q1 = 1000, Q2 = 1500 i Q3 = 2000 par butów dziennie, można wyznaczyć najbardziej efektywny zestaw czynników produkcji na podstawie następującego wykresu:
Krzywa jednakowego produktu (izokwanta) pokazuje, jakie kombinacje metod wytwarzania są niezbędne, aby wytworzyć tę samą wielkość produkcji. Krzywa jednakowego nakładu ilustruje, jakie kombinacje metod wytwarzania są możliwe do zastosowania po uwzględnieniu relacji cen obu czynników wytwórczych oraz wysokości zasobu środków finansowych, jakim dysponuje producent.
Nałóżmy krzywe jednakowego nakładu na „mapę" izokwant. Punktem optimum jest ten, który znajduje się na najwyżej usytuowanej izokwancie. Jest to punkt styczności krzywej jednakowego nakładu i izokwanty. Punkt ten jest oznaczony na rysunku symbolem e. Występuje wówczas optymalna, tzn. najlepsza z możliwych kombinacji czynników wytwórczych.
10 20 30 40 50 60 70 80
Liczba maszyn (M)
Liczba pracowników (L)
... zobacz całą notatkę




Komentarze użytkowników (0)