To tylko jedna z 9 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


Przykład 10.5. Obliczenie wska´ nika plastyczno´ ci przy skr˛ caniu
z
s
e
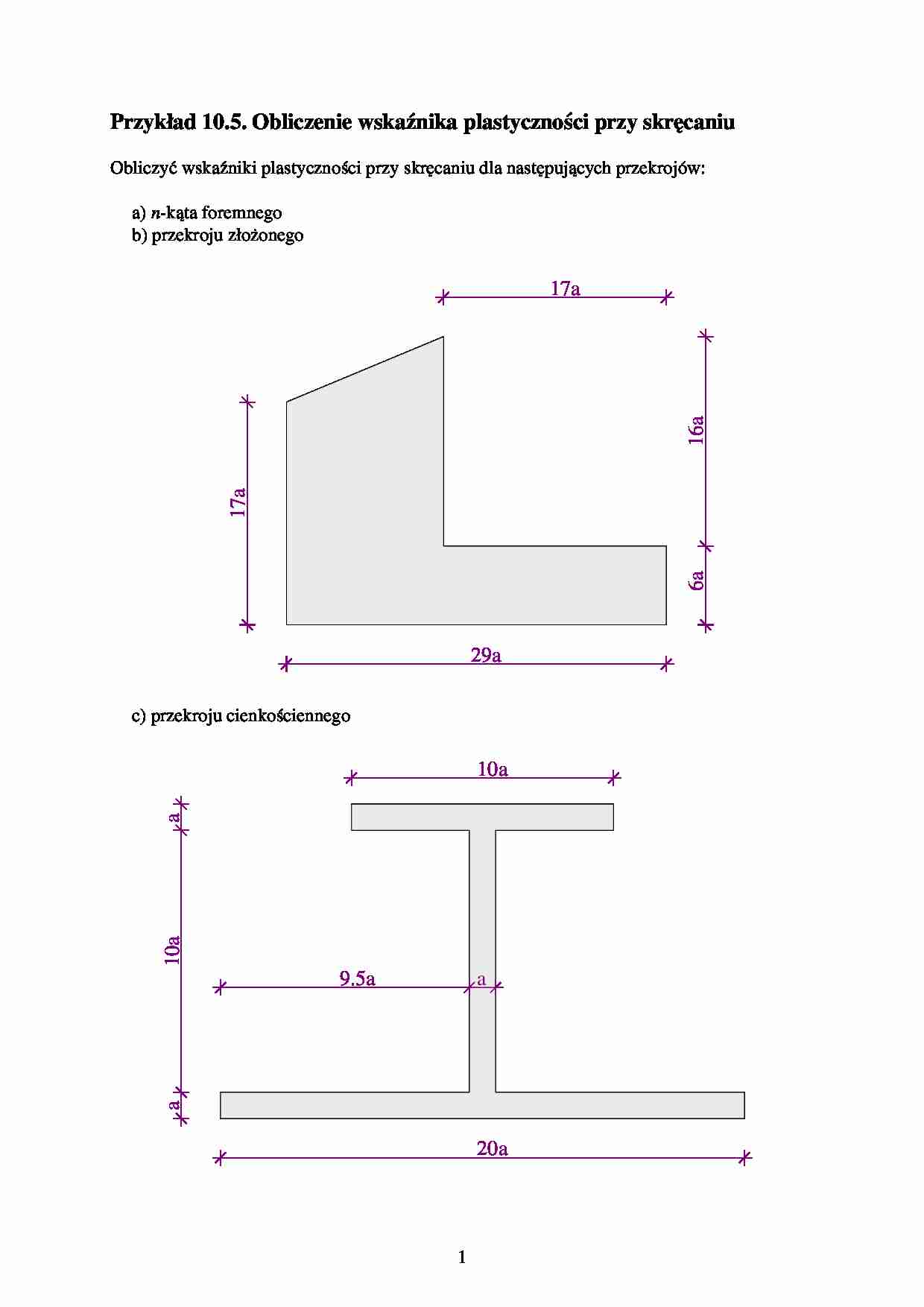
Obliczy´ wska´ niki plastyczno´ci przy skr˛ caniu dla nast˛ pujacych przekrojów:
c
z
s
e
e ˛
a) n-kata foremnego
˛
b) przekroju zło˙ onego
z
6a
17a
16a
17a
29a
c) przekroju cienko´ciennego
s
10a
a
10a
a
a
9.5a
20a
1
Rozwiazanie
˛
a) n-kat foremny
˛
Wska´ nik plastyczno´ci przy skr˛ caniu dla przekrojów jednospójnych mo˙ na łatwo policzy´
z
s
e
z
c
korzystajac z tzw. analogii Nadaia, zwanej równie˙ analogia wzgórza piaskowego. Zgodnie
˛
z
˛
z nia wska´ nik plastyczno´ci przy skr˛ caniu takiego przekroju równy jest podwojonej obj˛ to´ci
˛
z
s
e
e s
bryły powstałej poprzez nasypanie piasku na przekrój, je˙ eli kat u podstawy owej bryły wynosi
z
˛
45◦ .
r
a
h
Tak wi˛ c, w rozpatrywanym przypadku wska´ nik plastyczno´ci przy skr˛ caniu b˛ dzie równy
e
z
s
e
e
podwojonej obj˛ to´ci ostrosłupa o podstawie n-kata foremnego.
e s
˛
1
Wpl = 2V = 2 · SH
3
gdzie
V
S
H
−
−
−
obj˛ to´ c ostrosłupa
e s´
pole powierzchni podstawy
wysoko´ c ostrosłupa
s´
Rozpatrywany przekrój mo˙ na podzieli´ na n trójkatów, tak wi˛ c pole powierzchni n-kata foz
c
˛
e
˛
remnego jest równe:
1
S = n · ah
2
Poniewa˙ boku ostrosłupa tworza z podstawa kat 45◦ , wi˛ c zachodzi zale˙ no´ c
z
˛
˛ ˛
e
z s´
H =h
Je˙ eli zało˙ y´ , ze rozpatrywany wielokat mo˙ na wpisa´ w okrag o promieniu r, to prawda jest,
z
z c ˙
˛
z
c
˛
˛
ze
˙
sin
360◦
n
2
=
a
2
r
h
=
cos
2
r
360◦
n
=⇒
=⇒
180◦
n
180◦
h = r cos
n
a = 2r sin
2
Tak wi˛ c
e
n
180◦
180◦
n
180◦
180◦
1
· r cos
= · r 2 · 2 sin
cos
=
S = n · ah = · 2r sin
2
2
n
n
2
n
n
n
360◦
= r 2 sin
2
n
Obj˛ to´ c nasypanego ostrosłupa jest wi˛ c równa
e s´
e
1 n
360◦
180◦
n
360◦
180◦
1
· r cos
= r 3 sin
cos
V = Sh = · r 2 sin
3
3 2
n
n
6
n
n
Ostatecznie mo˙ na zapisa´ wzór na wska´ nik plastyczno´ci przy skr˛ caniu przekroju w kształz
c
z
s
e
cie n-kata foremnego:
˛
Wpl = 2V =
n 3
360◦
180◦
2
180◦
r sin
cos
= nr 3 sin
3
n
n
3
n
3
1 − sin2
180◦
n
b) przekrój zło˙ ony
z
6a
17a
16a
17a
29a
W celu obliczenia wska´ nika plastyczno´ci przy skr˛ caniu powy˙ szego przekroju ponownie
z
s
e
z
zastosujemy analogi˛ wzgórza piaskowego Nadaia.
e
Widok z góry usypanego wzgórza przedstawia poni˙ szy rysunek.
z
17a
6a
17a
16a
5a
12a
29a
Obliczenie obj˛ to´ci pokazanej bryły wymaga podzielenia jej na prostsze elementy.
e s
4
12a
17a
5a
B
z=
13a
y
A
16a
b
x
1.
E
C
D
3.
6a
4.
6.
5.
3a 3a
14a
6a
6a
2.
3a
Zgodnie z analogia Nadaia wska´ nik plastyczno´ci przy skr˛ caniu wynosi zatem
˛
z
s
e
Wpl = 2V = 2 (V1 + V2 + V3 + V4 + V5 + V6 )
Figura pierwsza jest ostrosłup o podstawie trapezu. Stad
˛
˛
˛
V1 =
1
· S 1 · h1
3
gdzie S1 oznacza pole podstawy ostrosłupa, a h1 jego wysoko´ c.
s´
Poniewa˙ kat nachylenia boków do podstawy ostrosłupa wynosi 45 ◦ to
z ˛
h1 =
12a
= 6a
2
´
Je´li oznaczymy wymiary ostrosłupa tak jak na rysunku poni˙ ej, to mo˙ emy zapisa c
s
z
z
S1 =
1
(b + b + 5a) · 12a = 6a (2b + 5a)
2
Nieznana długo´ c boków b
(…)
…
z
z
S1 =
1
(b + b + 5a) · 12a = 6a (2b + 5a)
2
Nieznana długo´ c boków b i z mo˙ na łatwo policzy´ wykorzystujac twierdzenie Pitagorasa,
˛
s´
z
c
˛
poniewa˙ trójkat ABD jest prostokatny, co wykazaqno poni˙ ej.
z
˛
˛
z
√
z 2 = (5a)2 + (12a)2
=⇒
z = 25a2 + 144a2 = 13a
Poniewa˙ katy nachylenia wszystkich boków bryły do podstawy sa równe, wi˛ c odcinki AD
z ˛
˛
e
i BD musza le˙ e´ na dwusiecznych…
… a
s
s´
b=
−5a + 13a
= 4a
2
Tak wi˛ c
e
S1 = 6a (2 · 4a + 5a) = 78a2
1
V1 = · 78a2 · 6a = 156a3
3
Bryła druga to graniastosłup o podstawie trójkatnej, którego obj˛ to´ c wynosi
˛
e s´
V2 =
1
· 12a · 6a · (17a − 4a − 6a) = 252a3
2
Bryła trzecia jest ostrosłup o podstawie prostokatnej.
˛
˛
˛
V3 =
1
· 6a · 12a · 6a = 144a3
3
Bryła czwarta to ostrosłup o podstawie trójkatnej, tak wi˛ c
˛
e
V4 =
1 1
· · 6a · 3a · 3a = 9a3
3 2
6
=⇒
Bryły piata i szósta to odpowiednio graniastosłup o podstawie trójkatnej i ostrosłup o podstawie
˛
˛
prostokatnej, stad
˛
˛
1
· 6a · 3a · (17a − 3a) = 126a3
2
1
V6 = · 6a · 3a · 3a = 18a3
3
V5 =
Ostatecznie wi˛ c obj˛ to´ c bryły nasypanego piasku jest równa
e
e s´
6
Vi = 156a3 + 252a3 + 144a3 + 9a3 + 126a3 + 18a3 = 705a3
V =
i=1
Stad szukany wska´ nik plastyczno´ci przy skr…
…
z
z
S1 =
1
(b + b + 5a) · 12a = 6a (2b + 5a)
2
Nieznana długo´ c boków b i z mo˙ na łatwo policzy´ wykorzystujac twierdzenie Pitagorasa,
˛
s´
z
c
˛
poniewa˙ trójkat ABD jest prostokatny, co wykazaqno poni˙ ej.
z
˛
˛
z
√
z 2 = (5a)2 + (12a)2
=⇒
z = 25a2 + 144a2 = 13a
Poniewa˙ katy nachylenia wszystkich boków bryły do podstawy sa równe, wi˛ c odcinki AD
z ˛
˛
e
i BD musza le˙ e´ na dwusiecznych…
... zobacz całą notatkę






Komentarze użytkowników (0)