To tylko jedna z 6 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
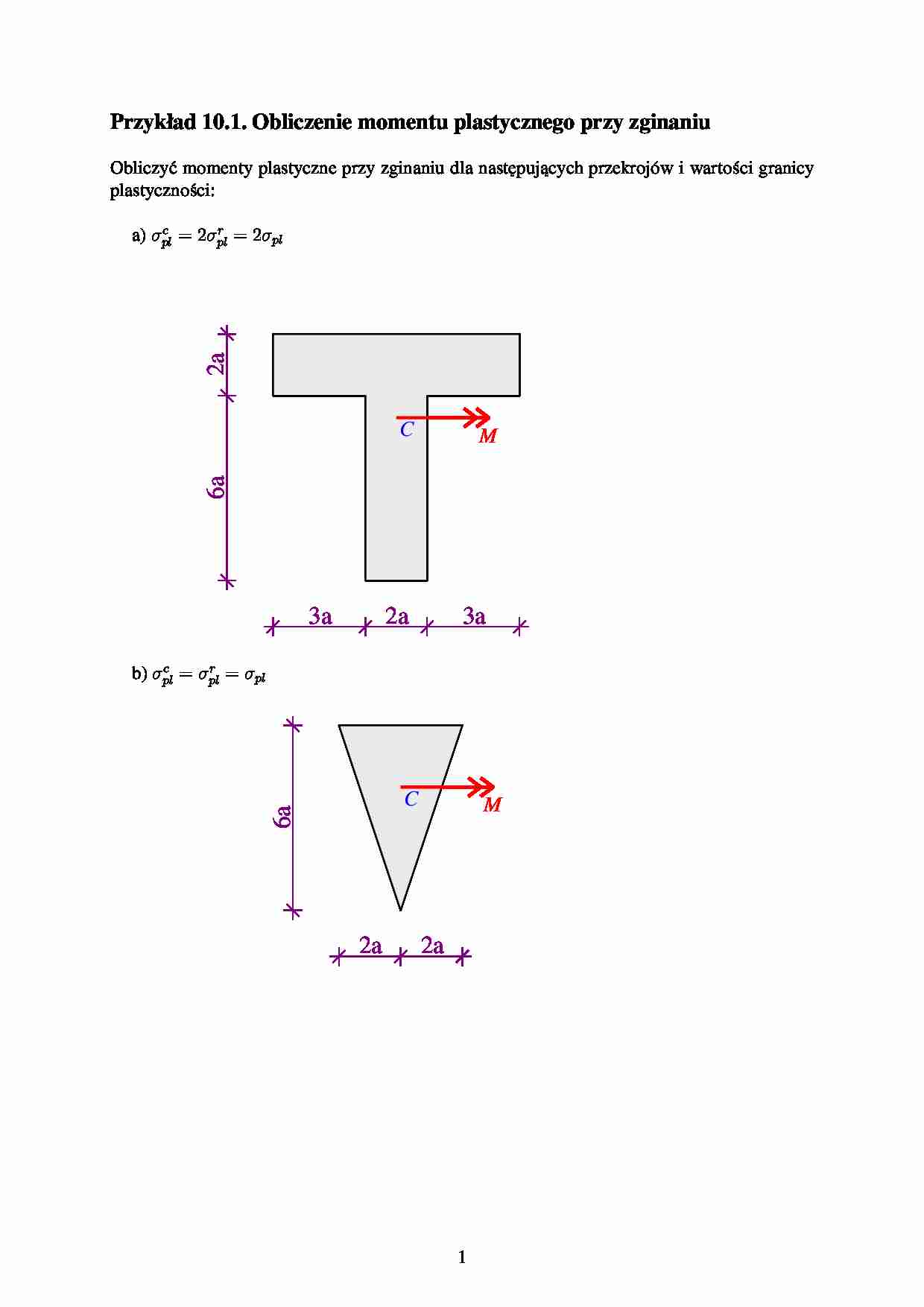


Przykład 10.1. Obliczenie momentu plastycznego przy zginaniu
Obliczy´ momenty plastyczne przy zginaniu dla nast˛ pujacych przekrojów i warto´ci granicy
c
e ˛
s
plastyczno´ci:
s
2a
c
r
a) σpl = 2σpl = 2σpl
C
6a
M
3a
2a
3a
r
c
b) σpl = σpl = σpl
6a
C
2a
M
2a
1
Rozwiazanie
˛
2a
c
r
a) σpl = 2σpl = 2σpl
C
6a
M
2a
3a
3a
Rozwiazywanie zadania zacza´ nale˙ y od okre´lenia poło˙ enia osi oboj˛ tnej w stanie pełnego
˛
˛c
z
s
z
e
uplastycznienia przekroju. Szukane poło˙ enie osi mo˙ na znale´ c z równania równowagi sił
z
z
z´
normalnych w przekroju. W dalszych obliczeniach zało˙ ono, ze szukana o´ oboj˛ tna przechodzi
z
˙
s
e
´
przez srodnik przekroju.
r
σ pl
Ar
x
M pl
d
Mpl
Ac
c
σ pl
y
r
c
σpl Ar = σpl Ac
=⇒
σpl Ar = 2σpl Ac
=⇒
Ar = 2Ac
gdzie
Ar
Ac
−
−
pole rozciaganej cz˛ sci przekroju
˛
e´
´
pole sciskanej cz˛ sci przekroju
e´
2
Poniewa˙
z
Ar + A c = A
gdzie
A = 2a · 8a + 6a · 2a = 28a2
−
pole przekroju poprzecznego
to
2Ac + Ac = A
1
Ac = A
3
=⇒
=⇒
Ac =
28 2
a
3
Stad
˛
Ac = 2a · d =
28 2
a
3
=⇒
d=
14
a
3
e
z
˛
z
e
Poniewa˙ d = 14 a
... zobacz całą notatkę






Komentarze użytkowników (0)