To tylko jedna z 17 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę

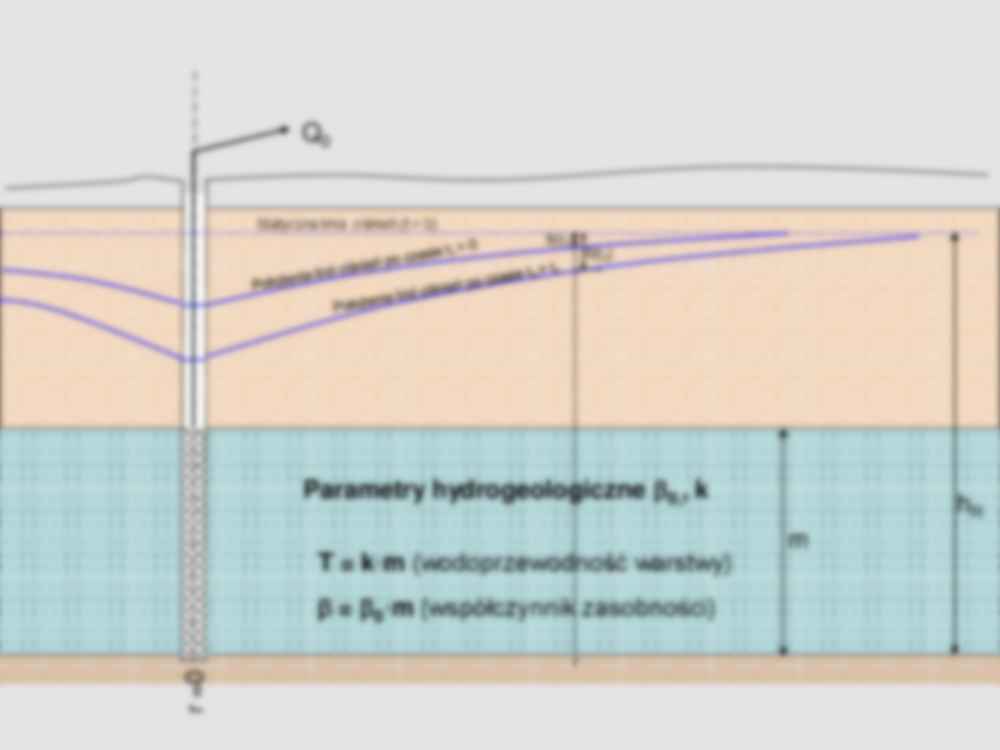

Nieustalony dopływ do studni (oraz do zespołu studni) m h R Q 0 Statyczna linia ciśnień (t = 0) Parametry hydrogeologiczne 0,, k T = k ·m (wodoprzewodność warstwy) = 0·m (współczynnik zasobności) r =0 S(t1) S(t2) r Równanie różniczkowe t T r r r 1 2 2 - potencjał Giryńskiego, [L2] r – odległość, [L] = 0·m współczynnik zasobności warstwy wodonośnej 0 – współczynnik zasobności sprężystej [L -1] m – miąższość warstwy wodonośnej [L] T = k ·m – wodoprzewodność warstwy wodonośnej, [L2T-1] k – współczynnik filtracji [LT-1] t – czas, [T] Warunki brzegowe i początkowe: const r R ) 0 , ( const t R ) , ( Rozwiązanie Theisa ) ( 4 4 0 0 u W k Q dx x e k Q R u x R W(u) – funkcja charakterystyczna studni ... ! 3 3 ! 2 2 ) ln( ) ( ) ( 3 2 u u u u u Ei dx x e u W u x tT r u 4 2 = 1.781 (stała Eulera) 0.0001 0.001 0.01 0.1 1 parametr charakterystyczny - u 0.1 1 10 F u n k c ja c h a ra k te ry s ty c z n a - W (u ) Wykres funkcji charakterystycznej studni - W(u) Rozwiązanie Theisa-Jacoba 2 0 2 0 0 0 0 25 . 2 lg 183 . 0 25 . 2 lg 3 . 2 4 1 ln 4 ) ln( ( 4 ) ( 4 r Tt T Q s r Tt T Q u T Q s u T Q u W T Q s Uproszczenie rozwiązanie Theisa dla długiego czasu pompowania (u
(…)
…
Theisa i Theisa–Jacoba
Metoda Theisa
Metoda TheisaJacoba
Współczynnik filtracji [m/s]
5.28 10-5
5.73 10-5
Współczynnik zasobności
sprężystej [m-1]
2.29 10-3
1.92 10-3
Parametr
Obliczenia depresji wywołanej eksploatacją zespołu studni w
warunkach nieustalonych
1. Przy pompowaniu krótkotrwałym (u > 0.05) należy korzystać z
rozwiązania Theisa, stosując zasadę superpozycji:
s
1
4 T
n
Q…
... zobacz całą notatkę






Komentarze użytkowników (0)