To tylko jedna z 4 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
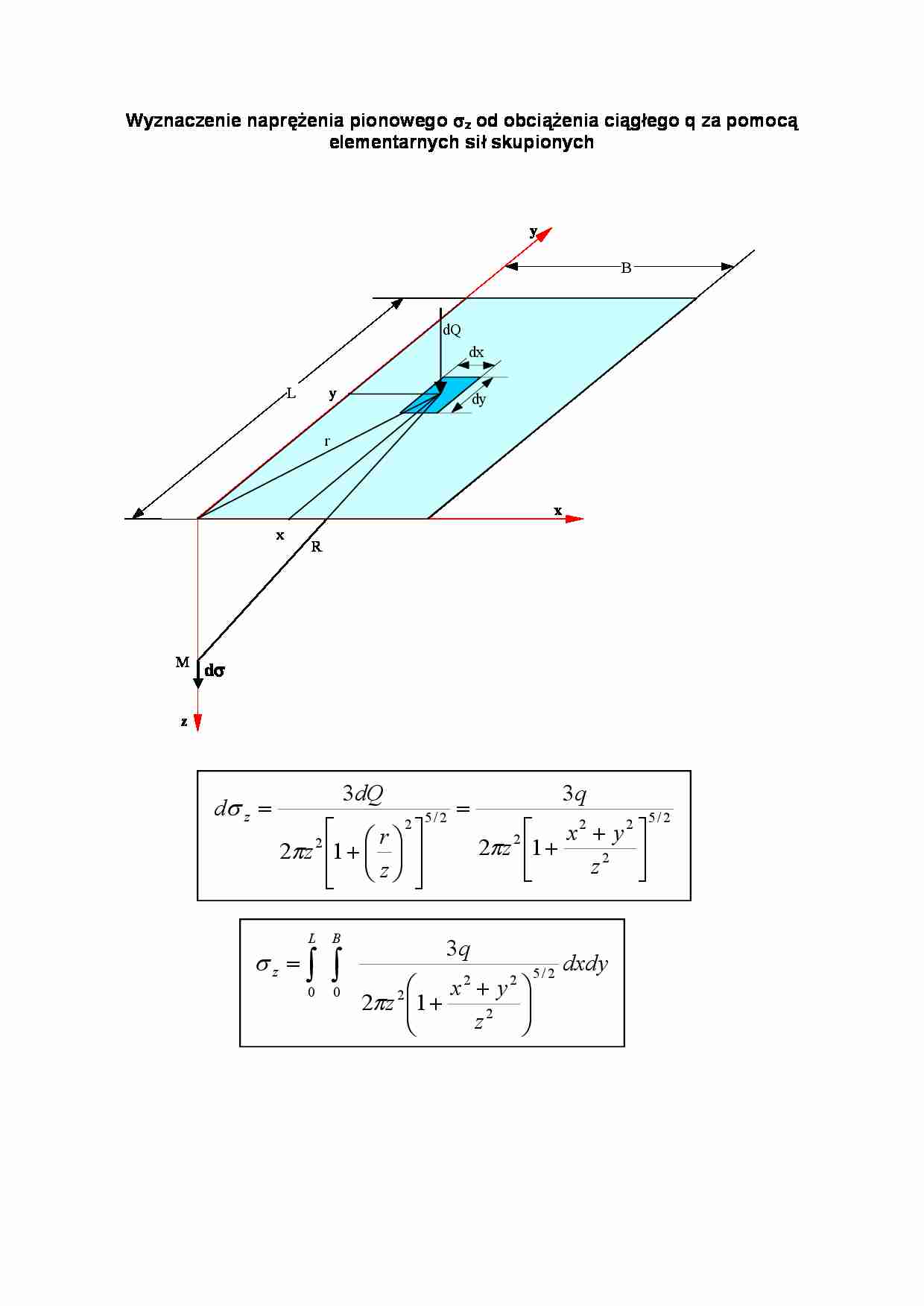


Wyznaczenie naprężenia pionowego sz od obciążenia ciągłego q za pomocą
elementarnych sił skupionych
y
B
dQ
dx
L
y
dy
r
x
x
M
R
ds
z
ds z =
3dQ
é æ r ö2 ù
2
2pz ê1 + ç ÷ ú
ê è zø ú
ë
û
L
sz = ò
0
B
ò
0
5/ 2
=
3q
é x2 + y2 ù
2pz ê1 +
z2 ú
ë
û
2
3q
æ x +y
2pz 2 ç1 +
ç
z2
è
2
2
ö
÷
÷
ø
5/ 2
dxdy
5/2
W przypadku gdy rozpatrywany punkt M znajduje się pod narożem obciążającej powierzchni
prostokątnej naprężenie pionowe w tym punkcie oblicza się ze wzoru:
s z = q×h n ,
gdzie:
ì
ùü
é
L
L z
ï
úï
ê
×
1 ï
1
1
B
B B
úï
ê
hn = íarctg
+
×
+
2
2
2 ý
2
2
2
2
2p ï
z
æ L ö æ z ö ê æ z ö æ L ö æ z ö úï
æ Lö æ z ö
1+ ç ÷ + ç ÷
1+ ç ÷ + ç ÷ ê 1 + ç ÷ ç ÷ + ç ÷ ú ï
ï
B
è B ø è B ø ë è B ø è B ø è B ø ûþ
èBø èBø
î
W przypadku gdy rozpatrywany punkt M znajduje się pod geometrycznym środkiem
obciążającej powierzchni prostokątnej naprężenie pionowe w tym punkcie oblicza się ze
wzoru:
s z = q×h0 ,
gdzie:
ì
ùü
é
L z
L
ï
2 ×
úï
ê
2ï
1
1
B B
B
úï
ê
h0 = íarctg
+
2×
2 +
2
2 ý
2
2
2
pï
ê
æ z ö æ Lö
æ z ö úï
z
æLö
æzö
æ Lö
æzö
2
1+ ç ÷ + 4 ç ÷
1 + ç ÷ + 4ç ÷ ê 1 + 4 ç B ÷ ç B ÷ + 4 ç B ÷ ú ï
ï
è ø è ø
è ø û
B
è Bø
èBø
èBø
èBø ë
î
þ
Nomogramy umożliwiające odczytanie wartości współczynnika zanikania naprężeń (η0)
przedstawiono na rys.1 nomogram do wyznaczania współczynnika (ηn) można znaleźć w
literaturze przedmiotu. Korzystniej jednak z uwagi na oszczędność czasu jak również ze
względu na dokładność jest wykorzystać specjalny program opracowany w formie skoroszytu
Excell, dostępny pod adresem:
http://www.ar.wroc.pl/~kajewski/dydaktyka/mechgrun/eta&eta0.xls
Rys. 1 Nomogram do wyznaczania współczynnika h0
Szczególną przydatność do obliczania naprężeń wywołanych prostokątnym obciążeniem
równomiernie rozłożonym posiada metoda punktów narożnych, zdefiniowana równaniem:
s z = q×h n ,
bowiem pozwala na obliczenie naprężeń w dowolnym miejscu półprzestrzeni gruntowej.
W przypadku, gdy rozpatrywany punkt M leży pod obrysem powierzchni prostokątnej należy
podzielić tak powierzchnię prostokątną, aby punkt ten stanowił naroże nowo utworzonych
prostokątów i posłużyć się następującym schematem:
L
L1
L2
B
A
C
B1
M
H
B
D
B2
G
E
F
s z = q×(h nMHAB +h nMBCD +h nMDEF +h nMFGH )
æ L1 z ö
, ÷ ; h nMBCD =
B1 B1 ÷
è
ø
gdzie: h nMHAB = f ç
ç
æL z ö
f ç 2 , ÷ ; h nMDEF =
çB B ÷
è 1 1ø
æL z ö
æL z ö
f ç 2 , ÷ ; h nMFGH = f ç 1 , ÷
çB B ÷
çB B ÷
è 2 2ø
è 2 2ø
W przypadku, gdy rozpatrywany punkt M leży poza obrysem powierzchni prostokątnej
należy wprowadzić dodatkowe powierzchnie prostokątne w taki sposób, aby punkt ten
stanowił naroże nowo powstałych prostokątów i posłużyć się następującym schematem:
L
L1
L2
M
H
D
B1
B
A
C
B2
B
G
E
F
s z = q × (h nMFGH +hnMDEF -hnMBAH -h nMDCB )
æL
z ö
gdzie: h nMFGH = f ç 1 , ÷ ;
çB B ÷
è 2 2ø
æ B2 z ö
æL z ö
æL z ö
, ÷ ; h nMBAH = f ç 1 , ÷ ; h nMDCB = f ç 2 , ÷
÷
çB B ÷
çB B ÷
è L2 B2 ø
è 1 1ø
è 1 1ø
h nMDEF = f ç
ç
... zobacz całą notatkę






Komentarze użytkowników (0)