To tylko jedna z 22 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę

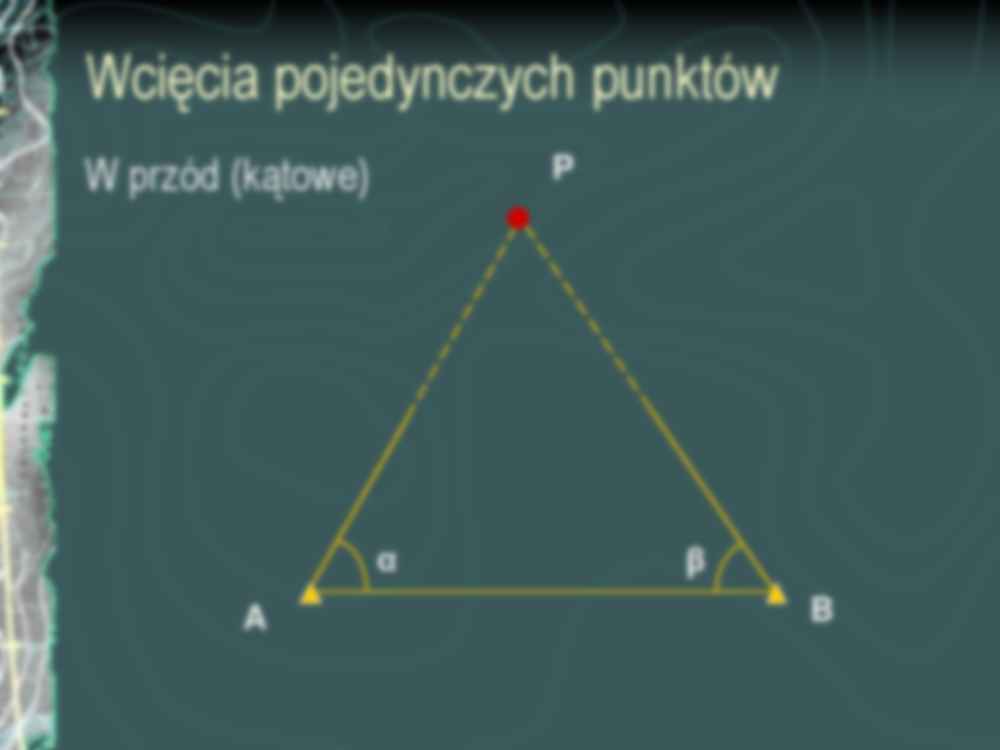
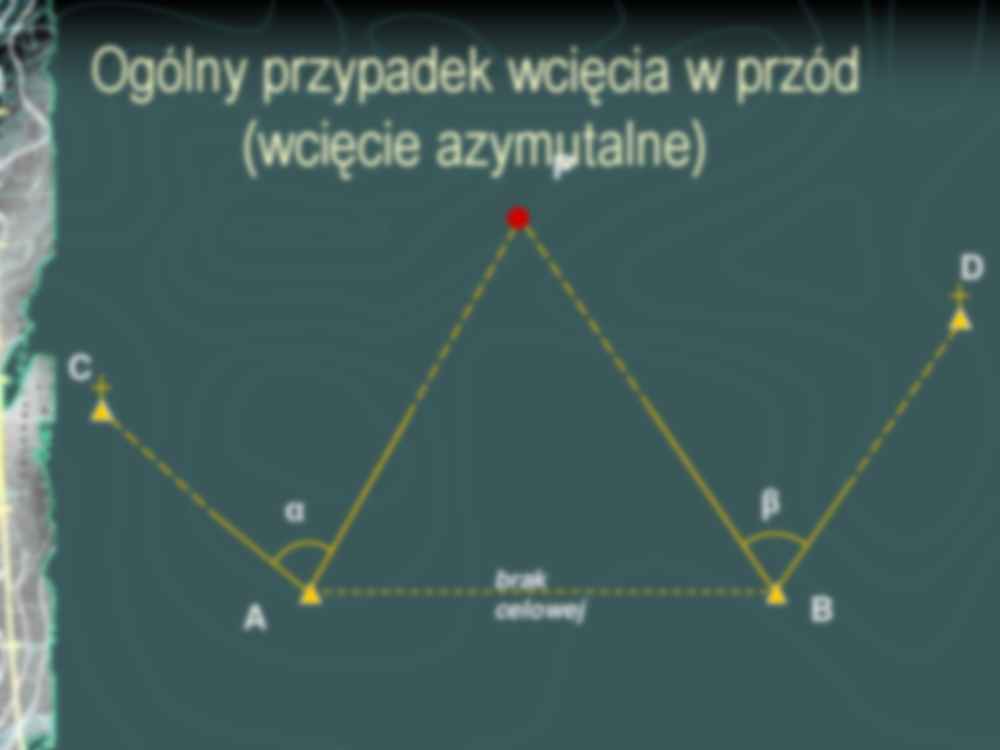
Metody zagęszczania osnowy szczegółowej - wcięcia Wcięcia wyznaczające jednoznacznie położenie punktów (bez kontroli pomiaru i wyrównania): - pojedynczych punktów (liniowe, w przód, w bok, kombinowane, wstecz) - par punktów (zadanie Hansena, Mareka) - wielopunktowe (złożone) Wcięcia z obserwacjami nadliczbowymi (możliwością wyrównania) - wcięcia dwustronne, - wolne stanowisko (free station) Wcięcia pojedynczych punktów W przód (kątowe) A P B β α Ogólny przypadek wcięcia w przód (wcięcie azymutalne) A P B β α C D brak celowej Wcięcie w bok A P B γ α Modyfikacja wcięcia w przód Wcięcie to ma inną charakterystykę dokładnościową niż wcięcie w przód ! Wcięcie kątowo-liniowe A P B γ α Modyfikacja wcięcia w bok – wcięcie kątowo-liniowe (kombinowane) – różne nazwy w podręcznikach Zamiast kąta γ mierzymy długość AP (d) Zaleta: obserwacje są wykonywane na punkcie wyznaczanym d Zalecane do zagęszczania osnowy pomiarowej Inne wcięcie kombinowane (zadanie ma dwa rozwiązania !) B sin ( γ) = sin (200 – γ) Zamiast kąta γ mierzymy długość PB (d) A P’ α d P . 200g - γ γ Wcięcie wstecz (zadanie Pothenota) Pomiar na punkcie wyznaczanym do punktów niedostępnych C P B β α α β A E D P W zależności od metody obliczeń przyjmuje się kąty lub kierunki Metoda Collinsa 1. Obliczyć współrzędne punktu Collinsa Q wcięciem w przód w oparciu o kąty α i β 2. Obliczyć kąty γ i δ z różnicy azymutów 3. Obliczyć współrzędne punktu P wcięciem w przód w oparciu o kąty γ i δ C A B β α P α β Q δ γ δ γ A QP = ABQ Wcięcie wstecz - wyznaczalność A Wcięcie niewyznaczalne wszystkie punkty na jednym okręgu C B β α P α β P Wcięcia wielopunktowe Par punktów: • zadanie Hansena • zadanie Mareka Złożone Liczba obserwacji n powinna być równa liczbie niewiadomych u u = 2 p gdzie: p – liczba punktów wyznaczanych Wcięcie wstecz na dwa punkty (zadanie Hansena) Pomiar na punktach wyznaczanych 3 wersje C P B β α α β A D P P Q Q Q β α γ δ γ γ δ δ
... zobacz całą notatkę






Komentarze użytkowników (0)