To tylko jedna z 13 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę

Metody i algorytmy optymalizacji dr Helena Spyra Wykład 2
PRZYBLIŻONE ROZWIĄZYWANIE RÓWNAŃ
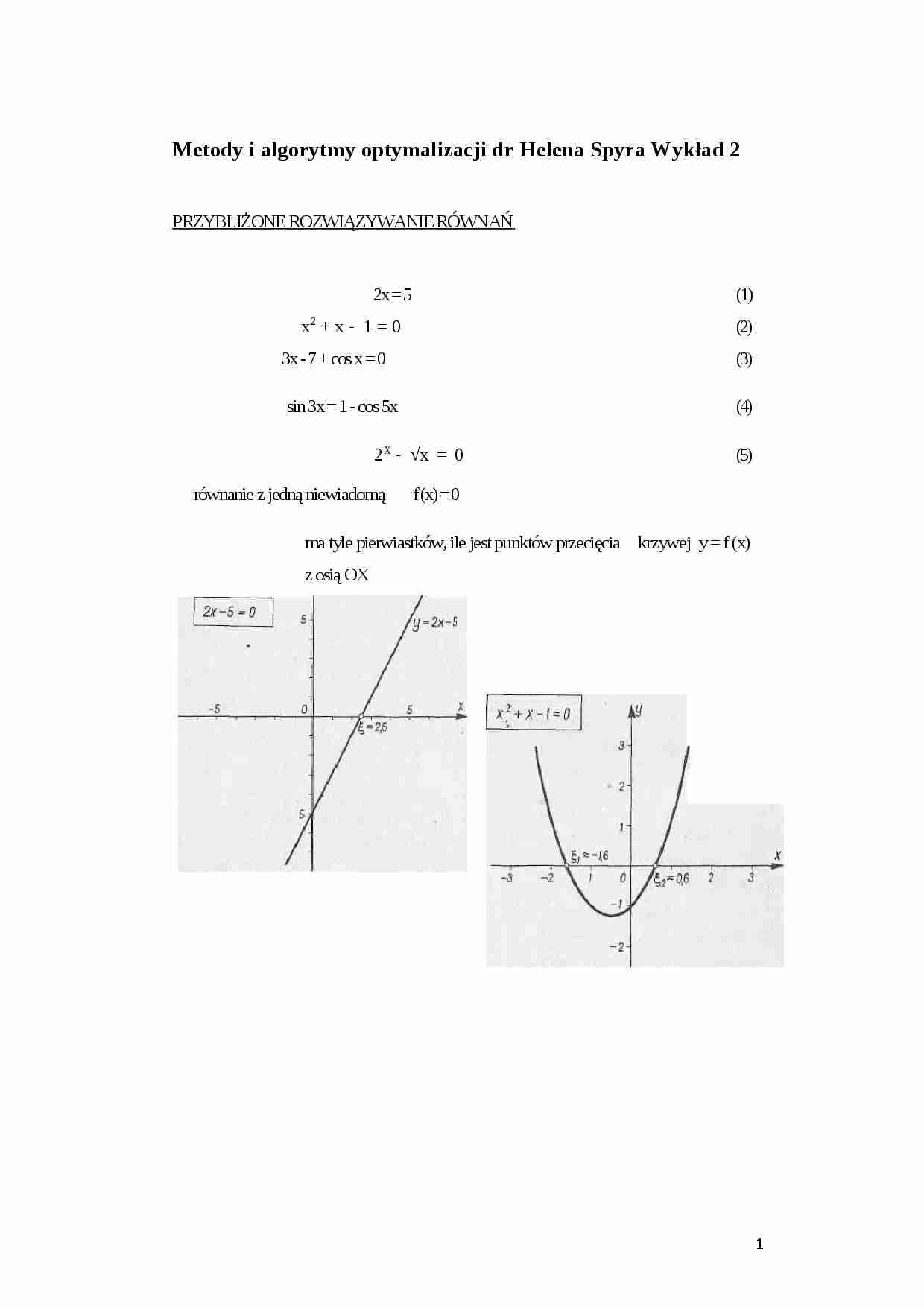
2x = 5 (1)
x2 + x - 1 = 0 (2)
3x - 7 + cos x = 0 (3)
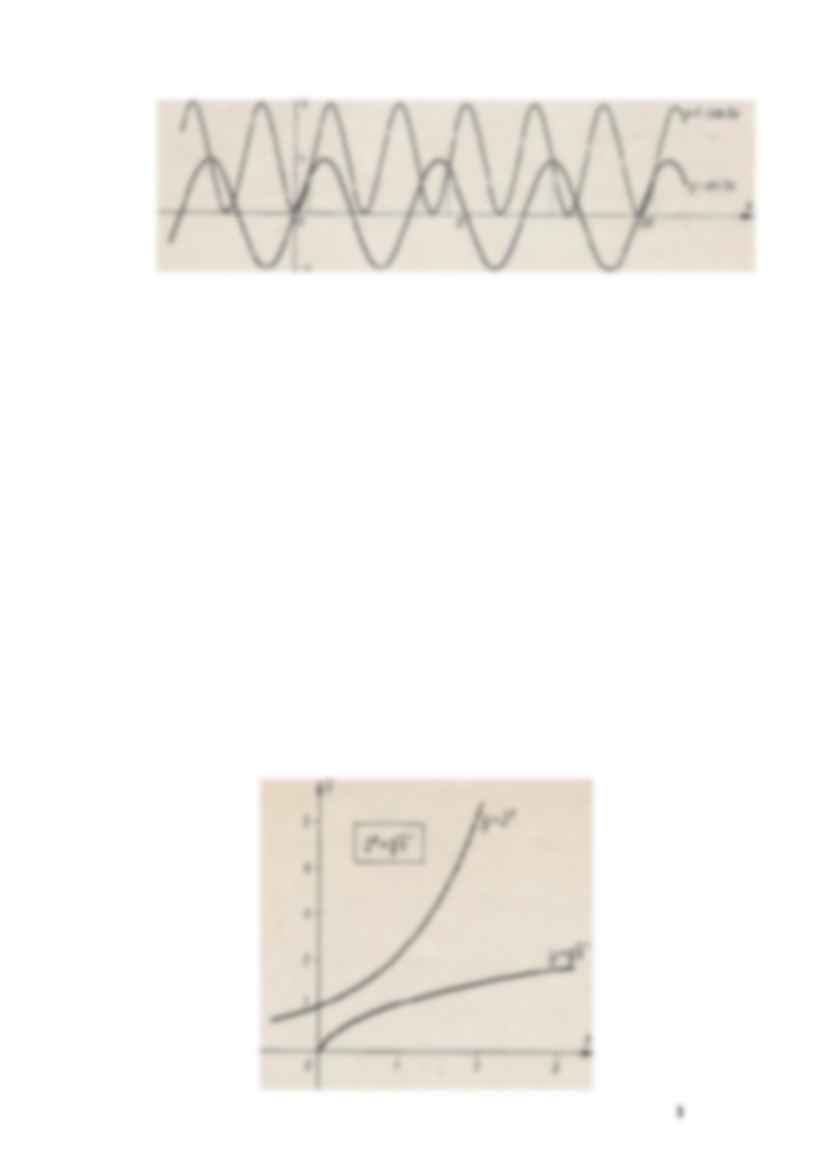
sin 3x = 1 - cos 5x (4)
2X- √x = 0 (5)
równanie z jedną niewiadomą f (x) = 0 ma tyle pierwiastków, ile jest punktów przecięcia krzywej y = f (x) z osią OX
sin3x = l-cosx
METODA ITERACJI równanie g (x ) = h (x ) układowi y = g (x) i y = h(x)
Załóżmy , że jedna z funkcji f (x) i h(x), np. funkcja h(x), ma funkcją odwrotną
x = h -1(y) = H (y)
układ równań równoważny:
y = g (x) x = H (y)
Niech x0 będzie przybliżoną wartością pierwiastka równania g (x) = h (x) znajdujemy: y1 = g(x0) x1 = H(y1)
y2 = g (x1) x2 = H (y2)
yn+1 = g (xn) xn+1 = H (yn+1)
jeśli ciąg liczb { xn } = x0, x1, x2,…
jest zbieżny, to jego granica jest szukanym pierwiastkiem. a) ciąg zbieżny b) ciąg rozbieżny
Warunkiem dostatecznym zbieżności ciągu jest spełniona w dostatecznie szerokim otoczeniu ξ
Przykład (3) 3x - 7 + cos = 0
g(x) = cos x h(x) = 7 - 3x
warunek spełniony jest na całej prostej. Funkcja h(x) ma funkcję odwrotną kolejne przybliżenia iteracyjne :
yn+1 = g(xn) = cos xn xn+1 = H(yn+1) = ⅓ (7 - yn+1)
Na podst. rys. jako wyjściowe przybliżenie przyjmujemy x0 = 2,65 y1 = cos 2,65 = -0,8815822
y2 = - 0,8705888 x2 = 2,6235296
y3 = - 0,8687800 x3 = 2,6229266
y4 = - 0,8684812 x4 = 2,6228271
y5 = - 0,8684319 x5 = 2,622816
y6 = -0,8684237 x6 = 2,6228079
(…)
… przybliżenia trzeba stosować specjalne metody.
REGUŁA FALSI, CZYLI METODA SIECZNYCH Niech będzie dane równanie f (x) = 0 i przedział [a,b] taki, że funkcja f (x) jest w nim ciągła i ściśle monotoniczna, a na końcach przedziału przyjmuje wartości o przeciwnych znakach. Równanie ma dokładnie jeden pierwiastek ξ w [a,b] .
Jako przybliżenie x1 przyjmiemy odciętą punktu dzielącego przedział [a,b] w stosunku
|f…
... zobacz całą notatkę






Komentarze użytkowników (0)