To tylko jedna z 19 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
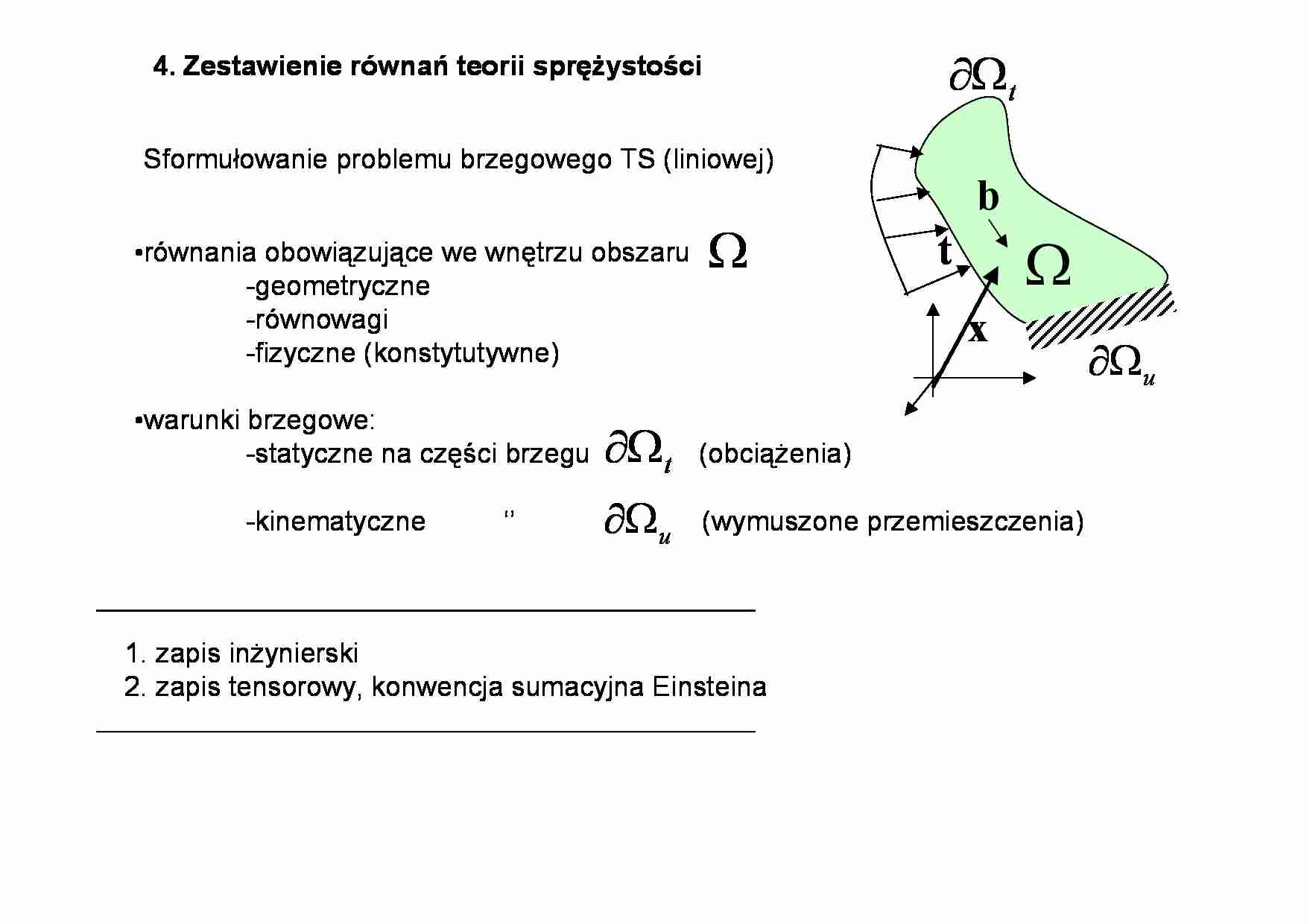


•równania obowiązujące we wnętrzu obszaru -geometryczne -równowagi -fizyczne (konstytutywne) •warunki brzegowe: -statyczne na części brzegu (obciążenia) -kinematyczne ‘’ (wymuszone przemieszczenia) 1. zapis inżynierski 2. zapis tensorowy, konwencja sumacyjna Einsteina 4. Zestawienie równań teorii sprężystości t Ω ∂ u Ω ∂ Sformułowanie problemu brzegowego TS (liniowej) t Ω t Ω ∂ u Ω ∂ b x Ω Siły zewnętrzne: siły masowe (grawitacja, etc.) siły powierzchniowe Dane: Szukamy pól: [ ] T Z Y X b b b = b ( ) ( ) j i j i x t x b k j i 3 , 2 , 1 , , = [ ] T Z Y X t t t = t pole wektorowe przemieszczeń ( ) j i x u ( ) [ ] T Z Y X u u u = x u A. zapis inżynierski ( ) k ij x ε ( ) k ij x σ pole tensorowe odkształceń pole tensorowe naprężeń ( ) ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ = ZZ YZ XZ YZ YY XY XZ XY XX σ σ σ σ σ σ σ σ σ x σ ( ) ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ = ZZ YZ XZ YZ YY XY XZ XY XX ε ε ε ε ε ε ε ε ε x ε Łącznie 15 nieznanych funkcji B.zapis tensorowy, konwencja sumacyjna Einsteina ; 0 0 0 ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ = + ∂ ∂ + ∂ ∂ + ∂ ∂ = + ∂ ∂ + ∂ ∂ + ∂ ∂ = + ∂ ∂ + ∂ ∂ + ∂ ∂ Z ZZ YZ XZ Y ZY YY XY X ZX YX XX b z y x b z y x b z y x σ σ σ σ σ σ σ σ σ które spełniają I. równania równowagi : (Naviera) [ ] Ω ∈ Ω ∈ = ∀ i T x z y x , , x 0 , = + j i ij b σ 3 równania różniczkowe o pochodnych cząstkowych (liniowe), 6 niewiadomych funkcji II. równania geometryczne (Cauche’go) ( ) i j j i ij u u , , 2 1 + = ε , 2 1 , 2 1 , 2 1 , , , ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ + ∂ ∂ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ + ∂ ∂ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ + ∂ ∂ = ∂ ∂ = ∂ ∂ = ∂ ∂ = z u y u x u z u x u y u z u y u x u Y Z YZ Z X XZ Y X XY Z ZZ Y YY X XX ε ε ε ε ε ε 3+6=9 równań różniczkowych o pochodnych cząstkowych (liniowych), 6+3+6=15 nieznanych funkcji III. równania fizyczne dla ciał izotropowych, liniowo-sprężystych – prawo Hooke’a kk ij ij ij G ε λδ ε
(…)
… izotropowych, liniowo-sprężystych – prawo Hooke’a
σ XX = 2Gε XX + λ (ε XX + ε YY + ε ZZ )
σ YY = 2Gε YY + λ (ε XX + ε YY + ε ZZ )
σ ZZ = 2Gε ZZ + λ (ε XX + ε YY + ε ZZ )
σ XY = 2Gε XY
σ XZ = 2Gε XZ
σ YZ = 2Gε YZ
G, λ −
σ ij = 2Gε ij + λδ ijε kk
stałe sprężystości, możliwe inne, równoważne sformułowania
6 równań algebraicznych, liniowych
razem 9+6=15 równań,
15 funkcji,
E , v, K
na brzegu obszaru spełniają…
... zobacz całą notatkę






Komentarze użytkowników (0)