To tylko jedna z 2 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
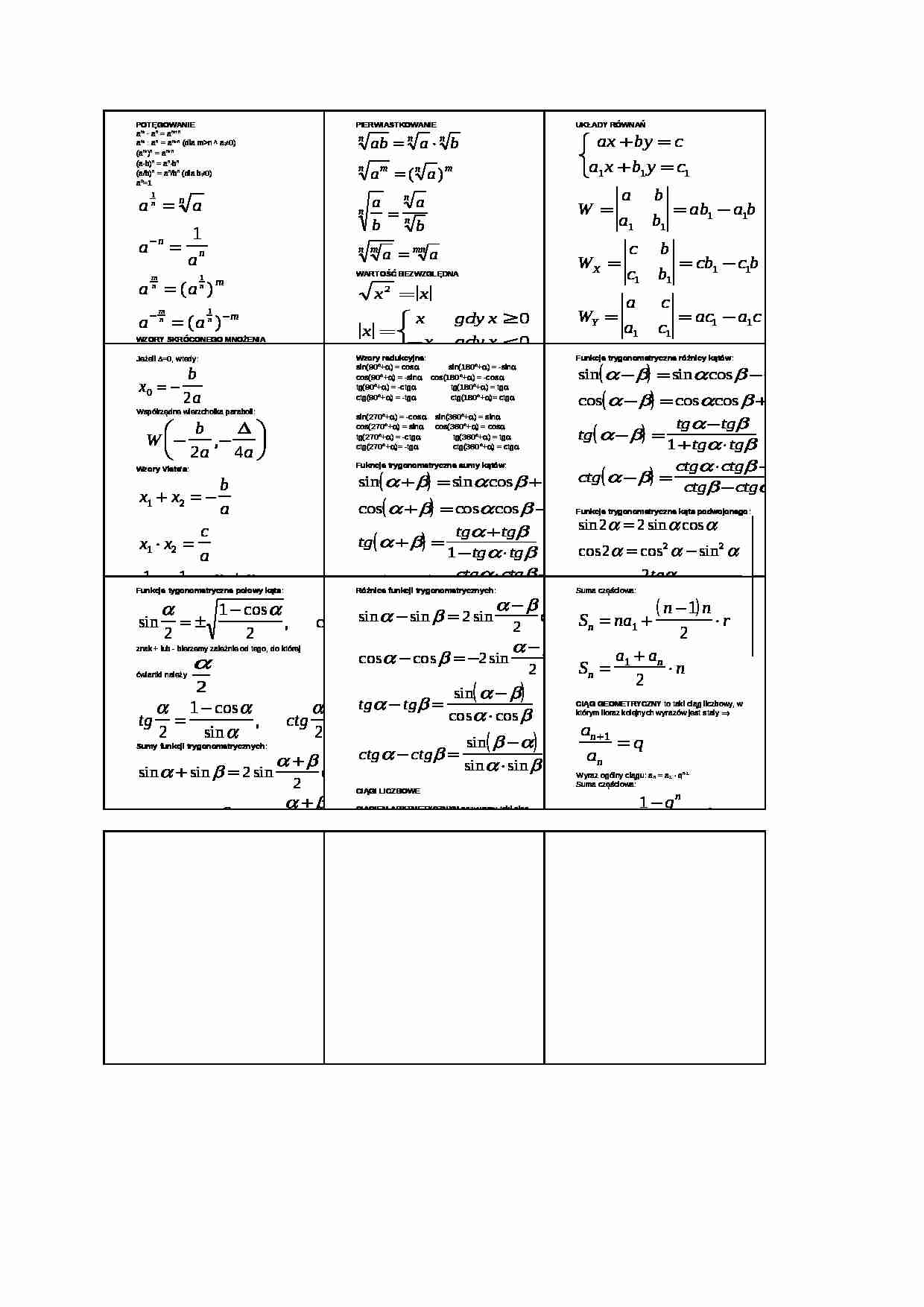

POTĘGOWANIE a m * a n = a m+n a m * a n = a m-n (dla mn * a≠0)
(a m ) n = a m ⋅ n (a⋅b) n = a n ⋅b n (a/b) n = a n /b n (dla b≠0)
a 0 =1
WZORY SKRÓCONEGO MNOŻENIA (a+b) 2 = a 2 +2ab+b 2 (a-b) 2 = a 2 -2ab+b 2 (a+b) 3 = a 3 +3a 2 b+3ab 2 +b 3 (a-b) 3 = a 3 -3a 2 b+3ab 2 -b 3 a 2 -b 2 = (a-b)(a+b)
a 3 -b 3 = (a-b)(a 2 +ab+b 2 )
a 3 +b 3 = (a+b)(a 2 -ab+b 2 )
PIERWIASTKOWANIE WARTOŚĆ BEZWZGLĘDNA RÓWNANIA I NIERÓWNOŚCI Z WARTOŚCIĄ BEZWZGLĘDNĄ Równanie: x-a= b, oznacza, że
x-a = b ∨ x-a = -b. Nierówność: x-a-b ∧ x-ab, jest spełniona ⇔ gdy:
x-ab UKŁADY RÓWNAŃ TRÓJMIAN KWADRATOWY f(x)=ax 2 +bc+c
Δ=b 2 -4ac
Jeżeli Δ0, wtedy: Jeżeli Δ=0, wtedy:
Współrzędne wierzchołka paraboli:
Wzory Viete'a :
TRYGONOMETRIA sin 2 α + cos 2 α = 1
tgα⋅ctgα = 1
Wzory redukcyjne :
sin(90°+α) = cosα sin(180°+α) = -sinα
cos(90°+α) = -sinα cos(180°+α) = -cosα
tg(90°+α) = -ctgα tg(180°+α) = tgα
ctg(90°+α) = -tgα ctg(180°+α)= ctgα
sin(270°+α) = -cosα sin(360°+α) = sinα
cos(270°+α) = sinα cos(360°+α) = cosα
tg(270°+α) = -ctgα tg(360°+α) = tgα
ctg(270°+α)= -tgα ctg(360°+α) = ctgα
Fukncje trygonometryczne sumy kątów :
Funkcje trygonometryczne różnicy kątów :
Funkcje trygonometryczne kąta podwojonego :
Funkcje tygonometryczne połowy kąta :
znak + lub - bierzemy zależnie od tego, do której ćwiartki należy Sumy funkcji trygonometrycznych :
Różnice funkcji trygonometrycznych :
CIĄGI LICZBOWE CIĄGIEM ARYTMETYCZNYM nazywamy taki ciąg liczbowy, w którym różnica kolejnych wyrazów jest stała ⇒ r =a n+1 - a n Wyraz ogólny ciągu: a n = a 1 + (n-1)r
Suma częściowa: CIĄG GEOMETRYCZNY to taki ciąg liczbowy, w którym iloraz kolejnych wyrazów jest stały ⇒ Wyraz ogólny ciągu: a n = a 1 ⋅ q n-1 Suma częściowa: Suma nieskończonego ciągu geometrycznego:
(…)
… ⇒ Wyraz ogólny ciągu: an = a1 ⋅ qn-1 Suma częściowa: Suma nieskończonego ciągu geometrycznego: POLA FIGUR PŁASKICH
Trójkąt:
S = pr, p - połowa obwodu; r - pr. okręgu wpisanego
, R - pr. okręgu opisanego
Trójkąt równoboczny:
Równoległobok:
Romb:
Trapez:
Koło i okrąg:
S = Πr2 2p = 2Πr p - połowa obwodu
Pole wycinka koła:
Długość łuku koła:
LOGARYTMY
STEREOMETRIA
Sześcian: V=a3 Prostopadłościan: V=abh
Walec: V=Πr2h
Ostrosłup foremny: V=1/3a2h
Stożek: V=1/3Πr2h, S-boczne=Πrl
Kula: V=4/3Πr3, S=4Πr2 GEOMETRIA ANALITYCZNA
Równanie prostej przechodzącej przez dwa punkty:
Odległość punktu od prostej:
Współczynnik kierunkowy:
Warunek równoległości: A1B2 = A2B1
Warunek prostopadłości: ac = -1
Wyznacznik (Dla trójkąta 1/2 det):
Iloczyn skalarny:
oblicznie długości wektorów z iloczynu skalarnego
OKRĄG
Równanie…
... zobacz całą notatkę




Komentarze użytkowników (0)