To tylko jedna z 24 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


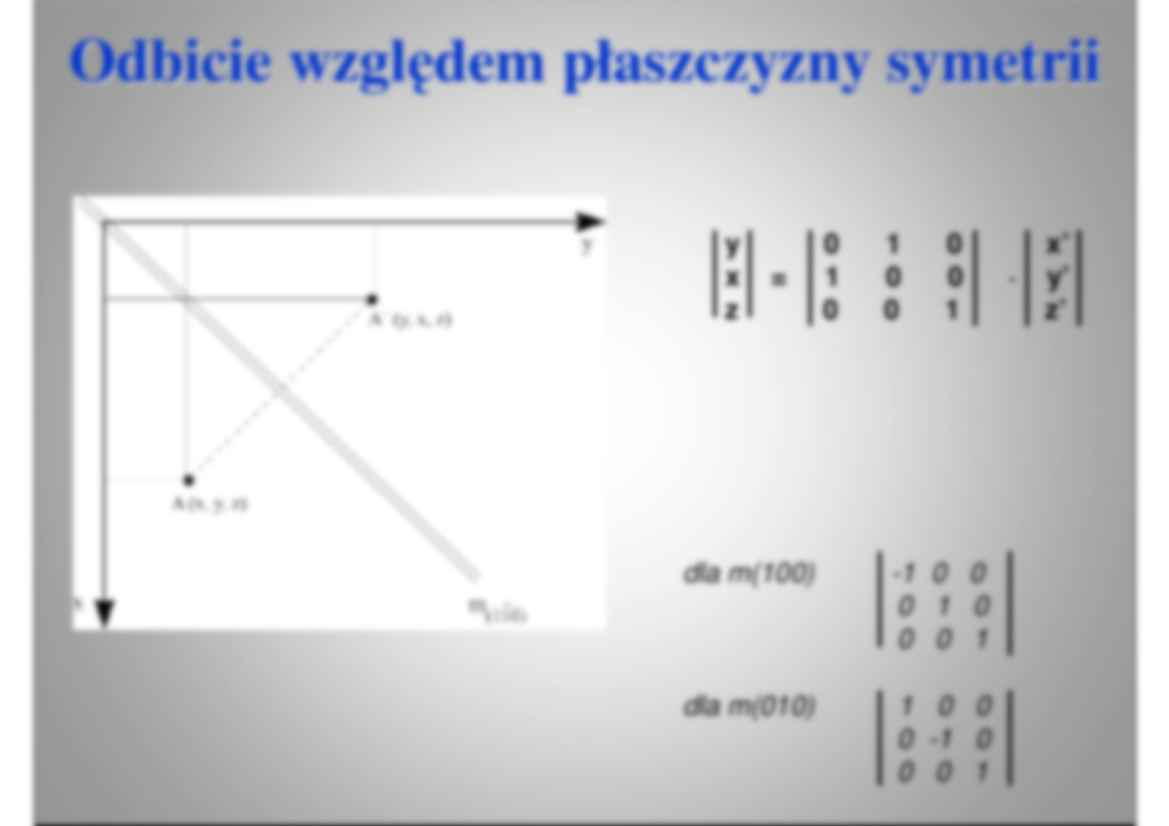
Wyk Wy ład 4 ad Symetria punktowa Symetria punktow 1. Macierze przekształce ń 2. Iloczyn i grupa przekształce ń 3. Grupa symetrii punktowej – klasy symetrii 4. Nomenklatura grup symetrii punktowej (klas symetrii) 5. Klasy symetrii a układy krystalograficzne 6. Podgrupy i super grupy symetrii Macierze przekszta Macierze przekszt łce c ń x` = a11x + a12y + a13z y` = a21x + a22y + a23z z` = a31x + a32y + a33z x` a11 a12 a13 x y` = a21 a22 a23 · y z` a31 a32 a33 z gdzie: x ,y, z – współrz ę dne wyj ś ciowe punktu P; x`, y` ,z` - współrz ę dne punktu P po przekształceniu (czyli punktu P`). dla m(100) -1 0 0 0 1 0 0 0 1 dla m(010) 1 0 0 0 -1 0 0 0 1 y 0 1 0 x’ x = 1 0 0 · y’ z 0 0 1 z’ Odbicie wzgl Odbicie wzg ę dem p dem łaszczyzny symetrii aszczyzny symetri Macierzowe reprezentacje r Macierzowe reprezentacje ó Ŝ nie nie po p ło Ŝ onych p onych łaszczyzn symetrii aszczyzn symetrii Płaszczyzna symetrii Macierz Płaszczyzna symetrii Macierz Płaszczyzna symetrii Macierz m(100) -1 0 0 0 1 0 0 0 1 m(010) 1 0 0 0 -1 0 0 0 1 m(001) 1 0 0 0 1 0 0 0 -1 m(110) 0 -1 0 -1 0 0 0 0 1 m( 110) 0 1 0 1 0 0 0 0 1 m(011) 1 0 0 0 0 -1 0 -1 0 m(101) 0 0 -1 0 1 0 -1 0 0 m( 101) 0 0 1 0 1 0 1 0 0 m(0 11) 1 0 0 0 0 1 0 1 0 Obr Ob ót dla kierunku [001] x = rcos α x` = rcos( α + ϕ ) y = rsin α y` = rsin( α + ϕ ) z = z z` = z x` = rcos α cos ϕ - rsin α sin ϕ y` = rcos α sin ϕ + rsin α cos ϕ z` = z x` = cos ϕ ·x + (-sin ϕ )·y + 0 y` = sin ϕ ·x + cos ϕ ·y + 0 z` = 0 + 0 + z [100] 1 0 0
(…)
…
I pozycja
II pozycja
III pozycja
1; 1
2║Y albo m⊥Y, albo
2║ i m⊥Y
2║X albo m⊥X
-
-
2║Y albo m⊥Y
6, 6, 3, ║Z albo
6, 3 ║Z i m⊥Z
2║X lub Y albo
m⊥X lub Y
4,4 ║Z albo
4║Z i m⊥Z
4,4, 2║ X, Y lub Z
albo m⊥X, Y, Z
2IIX lub Y
albo m⊥X lub Y
3║ [111]
3║ [111]
2║Z albo m⊥Z
2 ║ dwusiecznej kąta
między np.XY- albo
m⊥dwusiecznej kąta
między np.XY2║ [110] lub 2⊥[110]
2║ [110]
albo m⊥[110]
Podział klas symetrii…
…
trójskośny
1
1
jednoskośny
2
m
2/m
Układ rombowy
mm2
222
mmm
Układ tetragonalny
4
4
4mm
4/m
422
4mm
4/mm
Układ regularny
23
m3
432
43m
m3m
Układ heksagonalny
6
6
6/m
6/mm
_
6m2
622
6/mmm
3
3
3m
322
3m
Układ
Symbol
Trójskośny
1
1
2
m
2/m
Jednoskośny
32 klasy symetrii
oraz bryły je
charakteryzujące
Rombowy
Tetragonalny
Regularny
Heksagonalny
mm2
222
mmm
4
4
4/m
42m
4mm
422
4/m mm
23
m3
43m
432
m3m
3…
... zobacz całą notatkę






Komentarze użytkowników (0)