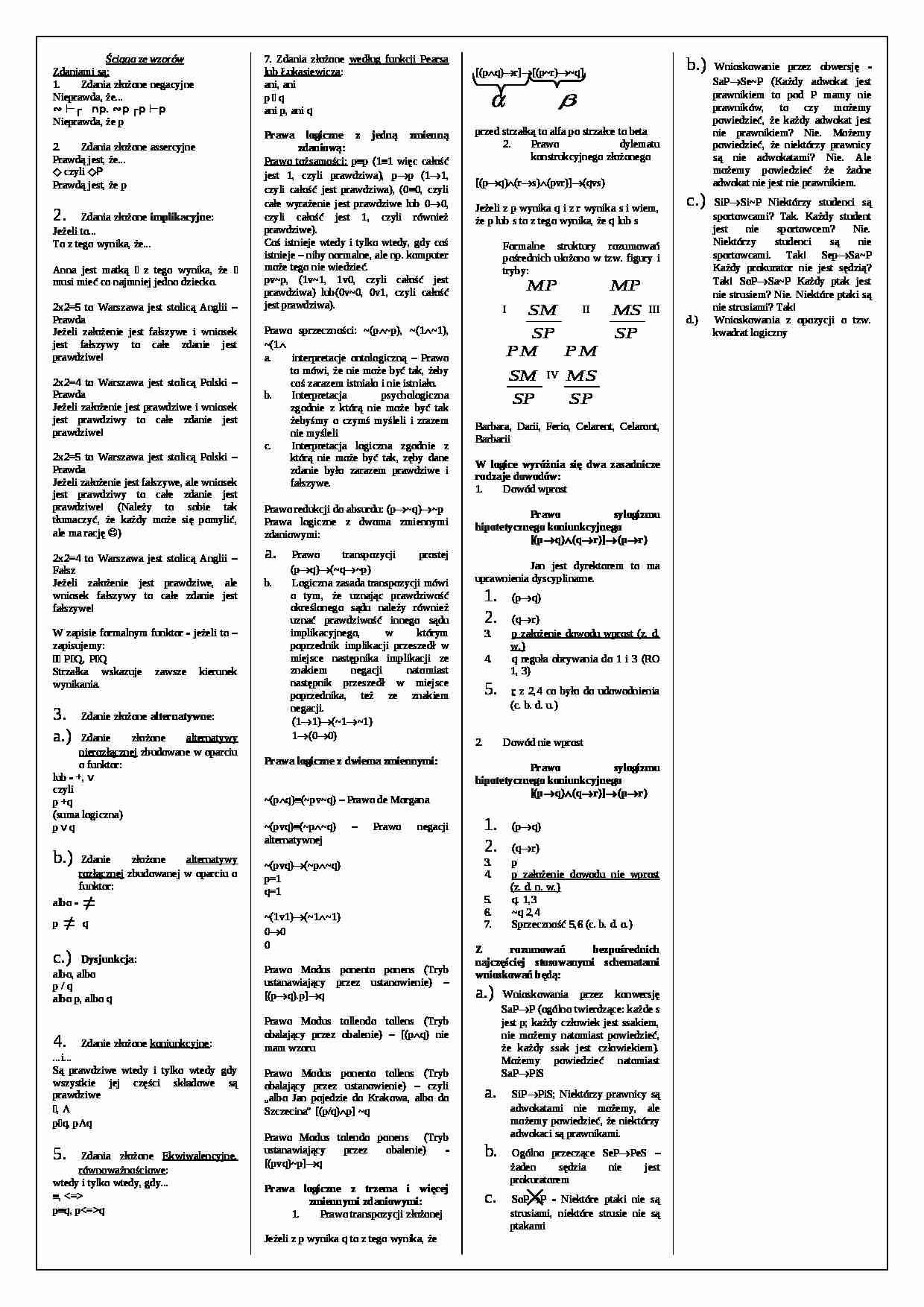
Dobre zestawienie jako zaplecze do nauki. Wzory dotyczą takich zagadnień jak: negacja, implikacja, alternatywa, dysjunkcja, prawo tożsamości, prawa logiczne z dwiema zmiennymi, prawa logiczne z trzeba i więcej zmiennymi zdaniowymi, dowód wprost, sylogizm hipotetyczny, kwadrat logiczny, prawo sylogizmu hipotetycznego kombinacyjnego.
Ściąga ze wzorów
Zdaniami są:
Zdania złożone negacyjne
Nieprawda, że...
∾ ⊢┌ np. ∾p ┌p ⊢p
Nieprawda, że p
Zdania złożone assercyjne Prawdą jest, że...
◇ czyli ◇P
Prawdą jest, że p
Zdania złożone implikacyjne:
Jeżeli to...
To z tego wynika, że...
Anna jest matką z tego wynika, że musi mieć co najmniej jedno dziecko.
2x2=5 to Warszawa jest stolicą Anglii - Prawda
Jeżeli założenie jest fałszywe i wniosek jest fałszywy to całe zdanie jest prawdziwe!
2x2=4 to Warszawa jest stolicą Polski - Prawda
Jeżeli założenie jest prawdziwe i wniosek jest prawdziwy to całe zdanie jest prawdziwe!
2x2=5 to Warszawa jest stolicą Polski - Prawda
Jeżeli założenie jest fałszywe, ale wniosek jest prawdziwy to całe zdanie jest prawdziwe! (Należy to sobie tak tłumaczyć, że każdy może się pomylić, ale ma rację )
2x2=4 to Warszawa jest stolicą Anglii - Fałsz
Jeżeli założenie jest prawdziwe, ale wniosek fałszywy to całe zdanie jest fałszywe!
W zapisie formalnym funktor - jeżeli to - zapisujemy: PQ, PQ
Strzałka wskazuje zawsze kierunek wynikania.
Zdanie złożone alternatywne:
Zdanie złożone alternatywy nierozłącznej zbudowane w oparciu o funktor:
lub - +, v
czyli
p +q
(suma logiczna)
p v q
Zdanie złożone alternatywy rozłącznej zbudowanej w oparciu o funktor:
albo - p q
Dysjunkcja:
albo, albo
p / q
albo p, albo q
Zdanie złożone koniunkcyjne: ...i...
Są prawdziwe wtedy i tylko wtedy gdy wszystkie jej części składowe są prawdziwe
, Λ
pq, pΛq
Zdania złożone Ekwiwalencyjne, równoważnościowe:
wtedy i tylko wtedy, gdy...
≡, <=>
p≡q, p<=>q
7. Zdania złożone według funkcji Pearsa lub Łukasiewicza:
ani, ani
p q
ani p, ani q
Prawa logiczne z jedną zmienną zdaniową:
Prawo tożsamości: p≡p (1≡1 więc całość jest 1, czyli prawdziwa), p→p (1→1, czyli całość jest prawdziwa), (0≡0, czyli całe wyrażenie jest prawdziwe lub 0→0, czyli całość jest 1, czyli również prawdziwe). Coś istnieje wtedy i tylko wtedy, gdy coś istnieje - niby normalne, ale np. komputer może tego nie wiedzieć.
pv~p, (1v~1, 1v0, czyli całość jest prawdziwa) lub(0v~0, 0v1, czyli całość jest prawdziwa).
Prawo sprzeczności: ~(p∧~p), ~(1∧~1), ~(1∧
interpretacje ontologiczną - Prawo to mówi, że nie może być tak, żeby coś zarazem istniało i nie istniało.
(…)
… i fałszywe.
Prawo redukcji do absurdu: (p→~q)→~p
Prawa logiczne z dwoma zmiennymi zdaniowymi: Prawo transpozycji prostej (p→q)→(~q→~p)
Logiczna zasada transpozycji mówi o tym, że uznając prawdziwość określonego sądu należy również uznać prawdziwość innego sądu implikacyjnego, w którym poprzednik implikacji przeszedł w miejsce następnika implikacji ze znakiem negacji natomiast następnik przeszedł w miejsce…
... zobacz całą notatkę


Komentarze użytkowników (0)