To tylko jedna z 83 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


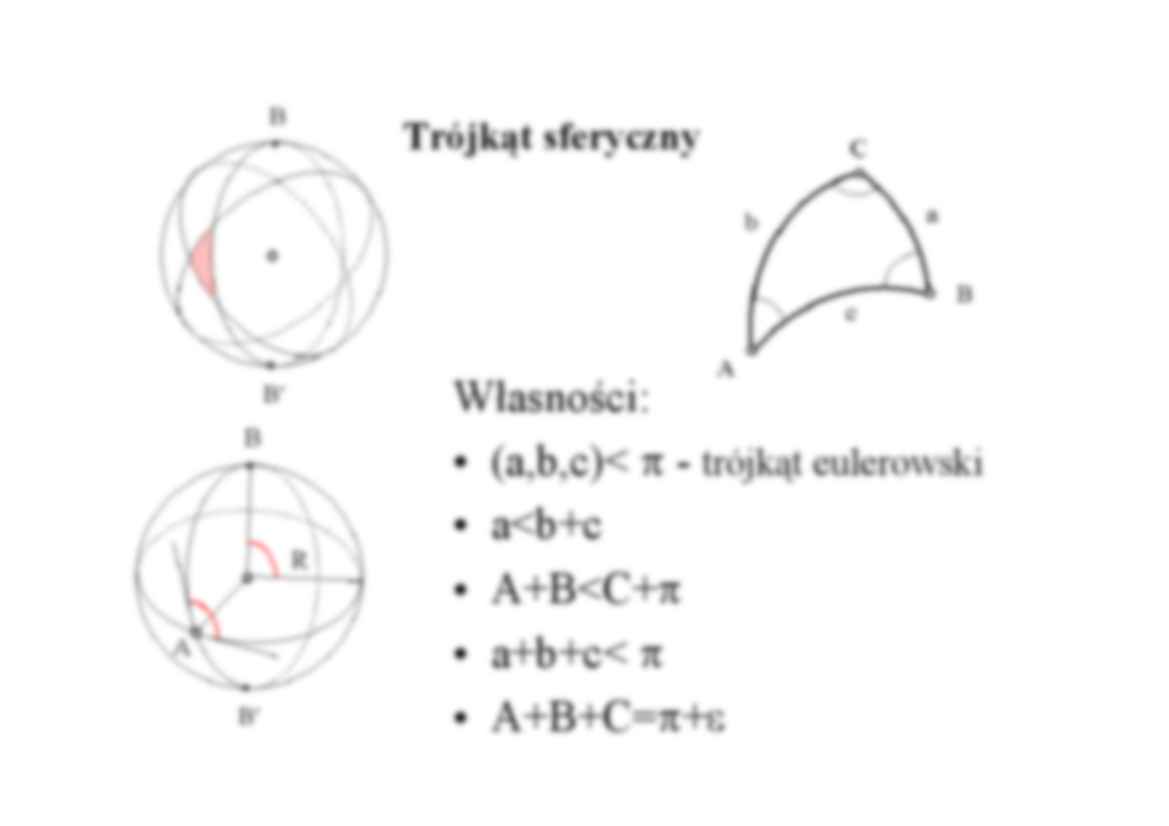
Kula jako powierzchnia odniesienia Elementy trygonometrii sferycznej – podstawowe pojęcia • Sfera /Kula • kula = sfera + wnętrze sfery, R Ziemia=6371 km • Koło na sferze - przekrój sfery płaszczyzną • koło wielkie i koło małe (przykłady) • Odległość sferyczna (w mierze liniowej i kątowej) • Biegun sfery • Trójkąt sferyczny Trójkąt sferyczny Własności: • (a,b,c)
(…)
…′ + δ b
A = A′
B = B′
c = c′ + δ c
C = C′
a3
δa = 2
6R
b3
δb = 2
6R
c3
δc = 2
6R
Układy współrzędnych na kuli
Układ współrzędnych geograficznych ϕ,λ,h
• Powierzchnia odniesienia
(R=6371km)
•
•
•
•
•
Oś układu,
Południk początkowy (zerowy),
ϕ ∈(0° ÷ 90°) N i (0° ÷ -90°) S
λ ∈ (0° ÷ 180°) E i (0° ÷ 180°) W
h – wzdłuż normalnej
Długość łuku południka i równoleżnika
• Łuk południka:
s p = R ⋅ ∆ϕ
• Łuk równoleżnika:
s r = r ⋅ ∆λ = R cosϕ ⋅ ∆λ
Układ współrzędnych prostokątnych XYZ
• Położenie środka układu i osi
względem powierzchni odniesienia,
• Układ prawoskrętny
• Warunek współrzędnych na
powierzchni kuli:
X 2 + Y 2 + Z 2 = R2
Związek współrzędnych XYZ
ze współrzędnymi geograficznymi ϕ,λ,h.
X = ( R + h) cos ϕ cos λ
(ϕ , λ , h) → ( X , Y , Z ) : Y = ( R + h) cos ϕ sin λ
Z = ( R + h) sin ϕ
Z
ϕ = arctg
X 2 +Y 2
Y
( X , Y , Z ) → (ϕ , λ , h) : λ = arctg
X
Z
h=
−R
sin ϕ
Układ współrzędnych biegunowych α,δ
•
•
•
•
Wybrany punkt główny P0(ϕ0λ0),
α - azymut koła wielkiego P0P,
δ - odległość sferyczna P0P,
(α,δ) ∈ (0°÷360°)
Związek między współrzędnymi geograficznymi (ϕ,λ)
i biegunowymi (α,δ)
Z wzoru cosinusowego i sinusowego:
cos δ = sin ϕ sin ϕ 0 − cos ϕ cos ϕ 0 cos(λ − λ0 )
sin(λ…
… sferyczny:
cos C = − cos A ⋅ cos B + cos A ⋅ cos B ⋅ cos c
• Nadmiar sferyczny (eksces) ε:
ε=
Pole∆ABC
R2
(dla ∆ eulerowskiego 0 < ε < 2π
)
ε
sin 12 a sin 12 b
sin C
Wzór Cagnoli: sin =
1 c
2
cos 2
Wzór L’Huiliera: tg
ε
s s −a s−b s−c
= tg tg
tg
tg
4
2
2
2
2
s=
a+b+c
2
Wzór przybliżony:
ε ≈ ε1 =
Pole∆ABC ( plaskiego ) bc sin A
=
2
R
2R 2
• Różnice miedzy wartościami ε policzonego ścisłym i
przybliżonym…
... zobacz całą notatkę






Komentarze użytkowników (0)