To tylko jedna z 11 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
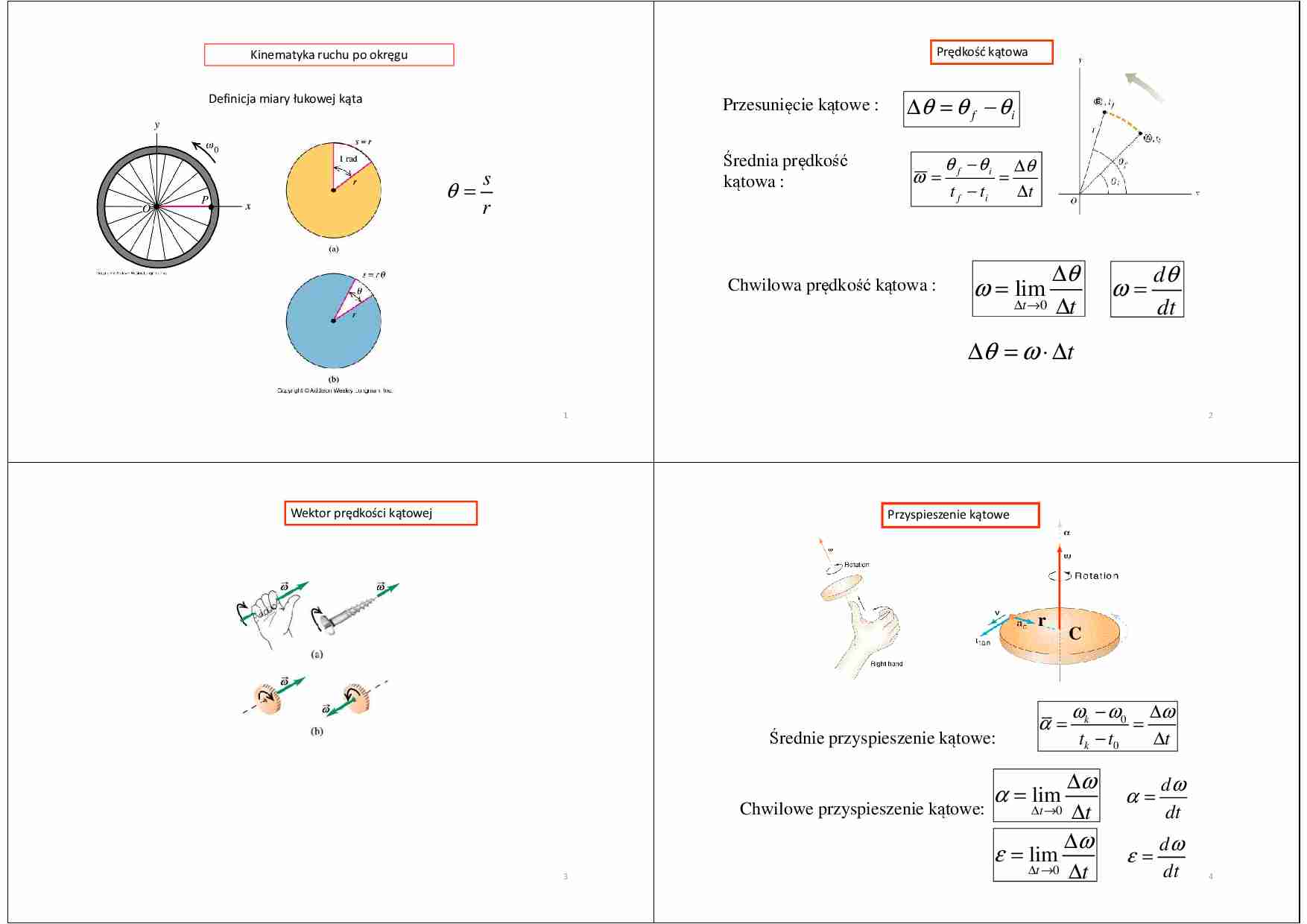


Prędkość kątowa
Kinematyka ruchu po okręgu
Przesunięcie kątowe :
s
θ=
r
∆θ = θ f − θ i
Średnia prędkość
kątowa :
Definicja miary łukowej kąta
ω=
Chwilowa prędkość kątowa :
θ f −θi
=
t f − ti
∆θ
∆t
∆θ
∆t →0 ∆t
ω = lim
dθ
dt
ω=
∆θ = ω ⋅ ∆t
1
Wektor prędkości kątowej
2
Przyspieszenie kątowe
r
Średnie przyspieszenie kątowe:
α=
ω k − ω0
t k − t0
∆ω
Chwilowe przyspieszenie kątowe:
∆t →0 ∆t
∆ω
ε = lim
∆t →0 ∆t
α = lim
3
C
=
∆ω
∆t
α=
dω
dt
ε=
dω
dt
4
Związek pomiędzy prędkością kątową i liniową
• stałe przyspieszenie kątowe –związek z prędkością i drogą kątową
s = rθ
r = const.
ω = co n s t.
α=
ω k − ω0
t k − t0
=
∆ω
∆t
v=
⇒
ωk = ω0 + α ⋅ ∆t
∆s
∆θ
=r
= rω
∆t
∆t
ω = ω0 + α ⋅ t
θ =ω 0t +
αt 2
2
5
6
Przyspieszenie styczne i dośrodkowe
Porównanie ruchów
ast = rα
Obrotowy
Liniowy
α = co nst
ast = rα
a = const
ω = ω0 + α t
v2
θ = θ 0 + ω 0t +
arad = 2
r
1
α t2
2
v = ωR
7
v = v0 + at
x = x0 + v 0t +
1 2
at
2
a = α R ; { ε = ωR }
8
v1
r1
r2
Ciała te poruszają się z różnymi
wartościami prędkości liniowej, lecz z tą
samą prędkością kątową ω.
m1
v =ωr
v2
m2
Energia kinetyczna układu
Ek =
(
1
1
1
2
2
m1v1 + m2 v2 = m1r12ω 2 + m2 r22ω 2
2
2
2
(
)
1
1
Ek = ω 2 m1r12 + m2 r22 = Iω 2
2
2
Moment bezwładności
(
I = m1r12 + m2 r22
)
∆miω 2 Ri2
∆EK i =
2
EK = ∆EK1 + ∆EK2 + ... + ∆EK N
EK =
)
ω2
( ∆m R
2
Iω 2
EK =
2
11
2
1 1
2
2
+ ∆m1 R2 + ... + ∆m1 RN )
Moment bezwładności względem osi równoległej do osi
przechodzącej przez środek masy
m r + ... + mn rn
=0
rcm = 1 1
m1 + ... + mn
Moment bezwładności względem osi przechodzącej
przez środek masy (punktu cm- początek u.w)
I cm = ∑ mi ( xi2 + yi2 )
i
d
Moment bezwładności względem osi
przechodzącej przez punkt P i równoległej do
osi przechodzącej przez środek masy
I p = Icm + M ⋅ d 2
I P = ∑ mi (( xi − a ) 2 + ( yi − b) 2 ) =
i
∑m (x
i
2
i
+ y ) − 2a ∑ mi xi − 2b ∑ mi yi + ( a 2 + b 2 ) ∑ mi
2
i
i
i
i
I p = Icm + M ⋅ d 2
przykład
I p = Icm + M ⋅ d 2
I CM =
2
MR 2
5
d
Ip =
2
MR 2 + Md 2
5
s Rθ
vcm = =
= Rω
t
t
1
1 2
Ek = I cmω 2 + mvcm
2
2
Ek =
1
1
I cmω 2 + mω 2 R 2
2
2
i
Toczenie się ciał po równi pochyłej
y
F
R
v = ωR oraz I = cMR2
Ekońcowa =
1
2
v
( cMR ) R
2
1 rura
1/2 walec
2/5 kula
c=
2
1
+ 2 Mv 2 =
1
2
( c + 1) Mv 2
Ekońcowa = E początkowa
1
2
( c + 1) Mv 2 = Mgh
v = 2gh
F
1
F
2
1
c +1
x
−F
∑F = 0
α ≠0
M = (−r × F ) + r × (− F )
α∝M
Moment siły
M = r ×F
i
j
k
r ×F = x
y
z
Fx
Fy
Fz
M
M = r F sin α
r × F = i ( yFz − zFy ) − j ( xFz − zFx ) + k ( xFy − yFx )
M = r ×F
Moment siły grawitacji
Druga zasada dynamiki dla ruchu obrotowego
Punkt materialny
Ft = mas
as = α ⋅ r
Ft = mrα ⋅ r
Ft r = mr 2α
M = Iα
24
Druga zasada dynamiki dla ruchu obrotowego
N
Jeżeli moment bezwładności nie ulega zmianie
ma = mg − N
N
R
F
M = r F sin φ
ma = mg − I
Ruch postępowy
F=
Iα = RN ; α R =a
a
N=I 2
R
M = Iα
∆p
; F = ma
∆t
Ruch obrotowy
M = Iα
a=
a
R2
mg
(…)
…
∆t
∆L
∆p
=v× p+r×
=r×F =M
∆t
∆t
∆L
=M
∆t
Ruch obrotowy wokół sztywno zamocowanej osi
Moment pędu
b) Dla bryły sztywnej obracającej się wokół sztywno zamocowanej osi
Lz = I ω
L = I ⋅ω
Druga zasada dynamiki dla ruchu obrotowego
Prawo zachowania momentu pędu
Jeżeli moment sił zewnętrznych jest równy zeru to
moment pędu jest zachowany
∆L
=M
∆t
∆L
=M
∆t
M =0 ⇔
Ruch postępowy
∆p
F=
; F = ma
∆t
∆L
=0
∆t…
... zobacz całą notatkę






Komentarze użytkowników (0)