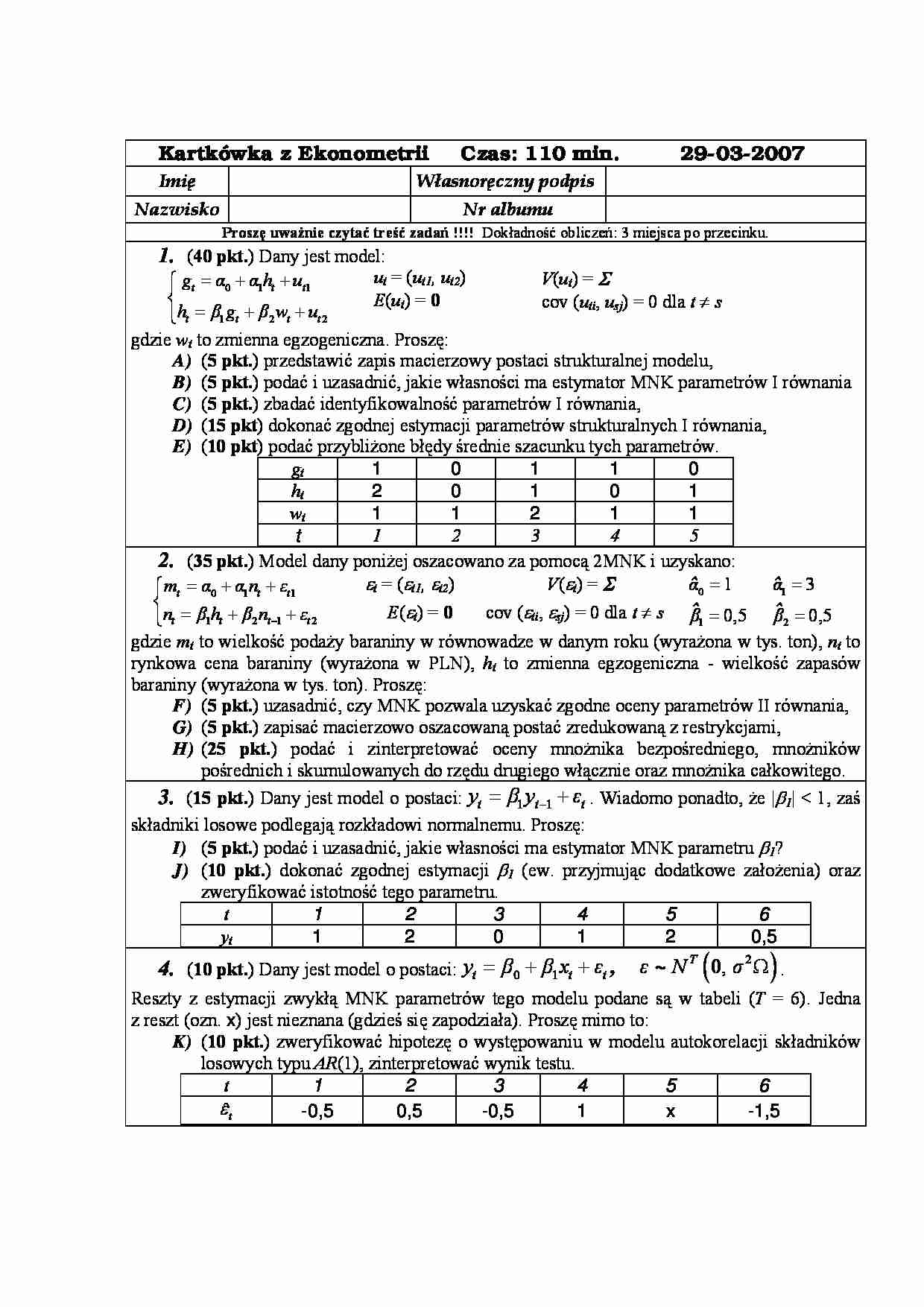
Kartkówka z Ekonometrii Czas: 110 min. 29-03-2007 Imię Własnoręczny podpis Nazwisko Nr albumu Proszę uważnie czytać treść zadań !!!! Dokładność obliczeń: 3 miejsca po przecinku. 1. ( 40 pkt. ) Dany jest model: ut = ( ut1, ut2 ) V ( ut ) = Σ E ( ut ) = 0 cov ( uti , usj ) = 0 dla t ≠ s gdzie wt to zmienna egzogeniczna. Proszę: A) ( 5 pkt. ) przedstawić zapis macierzowy postaci strukturalnej modelu, B) ( 5 pkt. ) podać i uzasadnić, jakie własności ma estymator MNK parametrów I równania C) ( 5 pkt. ) zbadać identyfikowalność parametrów I równania, D) ( 15 pkt ) dokonać zgodnej estymacji parametrów strukturalnych I równania, E) ( 10 pkt ) podać przybliżone błędy średnie szacunku tych parametrów. gt 1 0 1 1 0 ht 2 0 1 0 1 wt 1 1 2 1 1 t 1 2 3 4 5 2. ( 35 pkt. ) Model dany poniżej oszacowano za pomocą 2MNK i uzyskano: ε t = (ε t1, ε t2 ) V ( ε t ) = Σ 0 ˆ α = 1 ˆ α 1 = 3 E ( ε t ) = 0 cov ( ε ti , ε sj ) = 0 dla t ≠ s 0,5 0,5 gdzie mt to wielkość podaży baraniny w równowadze w danym roku (wyrażona w tys. ton), nt to rynkowa cena baraniny (wyrażona w PLN), ht to zmienna egzogeniczna - wielkość zapasów baraniny (wyrażona w tys. ton). Proszę: F) ( 5 pkt. ) uzasadnić, czy MNK pozwala uzyskać zgodne oceny parametrów II równania, G) ( 5 pkt. ) zapisać macierzowo oszacowaną postać zredukowaną z restrykcjami, H) ( 25 pkt. ) podać i zinterpretować oceny mnożnika bezpośredniego, mnożników pośrednich i skumulowanych do rzędu drugiego włącznie oraz mnożnika całkowitego. 3. ( 15 pkt. ) Dany jest model o postaci: 1 1 t t y β y ε − t = + . Wiadomo ponadto, że |β 1 |
(…)
… .
Reszty z estymacji zwykłą MNK parametrów tego modelu podane są w tabeli (T = 6). Jedna
z reszt (ozn. x) jest nieznana (gdzieś się zapodziała). Proszę mimo to:
K) (10 pkt.) zweryfikować hipotezę o występowaniu w modelu autokorelacji składników
losowych typu AR(1), zinterpretować wynik testu.
t
1
2
3
4
5
6
εt
ˆ
-0,5
0,5
-0,5
1
x
-1,5
…
... zobacz całą notatkę



Komentarze użytkowników (0)