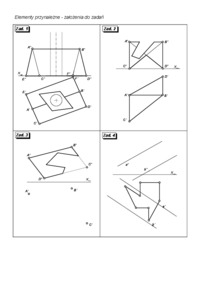
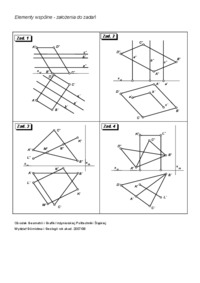
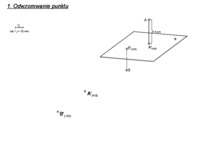
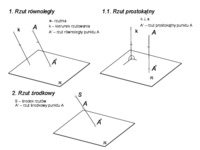
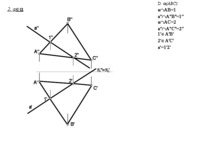
ĆWICZENIE KLAUZUROWE Odwzorowanie płaszczyzny prostopadłej do rzutni poziomej lub pionowej (π1 lub π2). Kład płaszczyzny. Przykłady zadań: I. Dane są rzuty odcinka AB. 1. Wyznaczyć rzuty kwadratu ABCD, którego płaszczyzna jest prostopadła do rzutni poziomej. 2. Wyznaczyć rzuty
ĆWICZENIE KLAUZUROWE NR 3 Elementy przynależne 1. Dane są rzuty zadaszenia składającego się z dwóch równoległoboków o wspólnej krawędzi AB. Wyznaczyć rzut pionowy otworu wykonanego w zadaszeniu. Ustalić widoczność krawędzi dachu i otworu u...
ĆWICZENIE KLAUZUROWE NR 4 Elementy wspólne 1. Wyznaczyć linię przenikania rynny, w postaci dwóch płaszczyzn ograniczonych prostymi a, b i c (prosta a jest częścią wspólną obu płaszczyzn), z płaszczyzną równoległoboku ABCD. 2. Dane są płaszczyzny naroża budowli określone prostymi a, b i c oraz ...
ĆWICZENIE KLAUZUROWE NR 5 Elementy prostopadłe 1. Dane są rzuty punktu P oraz płaszczyzny trójkąta ABC. Wyznaczyć rzuty punktu Q, tak aby powstały odcinek PQ był symetryczny względem danej płaszczyzny ABC. 2. Dane są rzuty odcinka AB należąc...
ĆWICZENIE KLAUZUROWE NR 6 Transformacja układu odniesienia 1. Dane są rzuty trójkąta ABC, którego bok AC jest równoległy do rzutni poziomej. Wyznaczyć rzuty graniastosłupa prostego, którego podstawą jest dany trójkąt. Długość krawędzi bocznych jest równa długości odcinka AC. 2. Dane są rzuty p...
ĆWICZENIE KLAUZUROWE NR 11 1. Dany jest rzut prostej a oraz punktu K, należącego do tej prostej. Wyznacz rzut odcinka KL należącego do prostej a o długości 6 cm. 2. Dany jest rzut punktu T oraz prostej a o nachyleniu 2/3. Wyznacz rzut prostej b, równoległej do prostej a przechodzącej przez punk...
Rsi PRACA SEMESTRALNA 2 arkusze formatu A3 TREŚĆ ZADANIA Na przyjętym indywidualnie planie warstwicowym terenu, zaprojektować poziomy plac o powierzchni 800 – 1200 m2 z drogą dojazdową w spadku. Dane: • Nachylenie drogi 10% • nachylenie wykopów 1/1 lub 2/3 • nachylenie nasypów 2/3 lub 1...
Temat: Rzut cechowany 1. Odwzorowanie punktu A 1j lub 1 j = 10 mm 4 cm π B'(-3,5) B A'(4,0) B'(-3,5) A'(4,0) 2. Odwzorowanie prostej 2.1. Prosta w położeniu ogólnym 1j a' A'(5,3) 1, 3 4 m 3 a m a 2 1 0 B'(-0,5) Nachylenie prostej a 3 j 2 j 1 ϕ 0 j j j j j ...
Temat: Rzutowanie 1. Rzut równoległy k⊥π π– rzutnia k – kierunek rzutowania A' – rzut równoległy punktu A k ~ 1.1. Rzut prostokątny ~ A' – rzut prostokątny punktu A k ...
Temat: Metoda rzutów Monge’a Elementy przynależne D: α(ABC) 2. a∈α a∩AB=1 a''∩A''B''=1'' a∩AC=2 a''∩A''C''=2'' 1'∈A'B' 2'∈A'C' a'=1'2' B'' a'' 1'' A'' 2'' C'' π1"=π2' 2' A' C' 1' a' B' D: A''B''C''D'' A'B'C' Konstrukcja
