To tylko jedna z 2 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
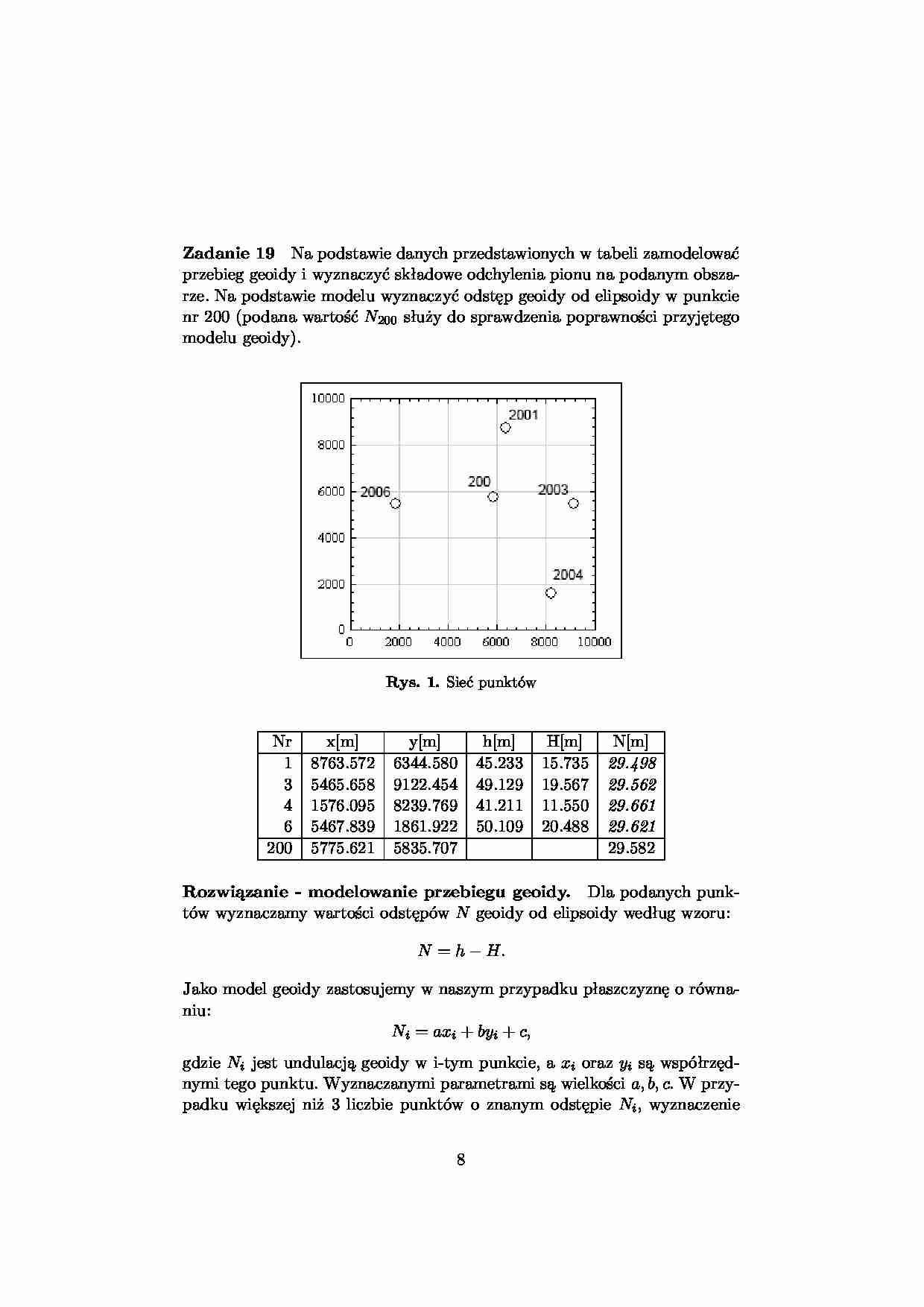

Zadanie 19 Na podstawie danych przedstawionych w tabeli zamodelować przebieg geoidy i wyznaczyć składowe odchylenia pionu na podanym obsza- rze. Na podstawie modelu wyznaczyć odstęp geoidy od elipsoidy w punkcie nr 200 (podana wartość N 200 służy do sprawdzenia poprawności przyjętego modelu geoidy). Rys. 1. Sieć punktów Nr x[m] y[m] h[m] H[m] N[m] 1 8763.572 6344.580 45.233 15.735 29.498 3 5465.658 9122.454 49.129 19.567 29.562 4 1576.095 8239.769 41.211 11.550 29.661 6 5467.839 1861.922 50.109 20.488 29.621 200 5775.621 5835.707 29.582 Rozwiązanie - modelowanie przebiegu geoidy. Dla podanych punk- tów wyznaczamy wartości odstępów N geoidy od elipsoidy według wzoru: N = h − H. Jako model geoidy zastosujemy w naszym przypadku płaszczyznę o równa- niu: Ni = axi + byi + c, gdzie Ni jest undulacją geoidy w i-tym punkcie, a xi oraz yi są współrzęd- nymi tego punktu. Wyznaczanymi parametrami są wielkości a, b, c . W przy- padku większej niż 3 liczbie punktów o znanym odstępie Ni , wyznaczenie 8 parametrów a, b, c przeprowadzimy metodą najmniejszych kwadratów zgod- nie z zależnością; x = − ( A T A ) − 1 A T L , gdzie macierze A i L : A = x 1 y 1 1 .. . .. . .. . xn yn 1 , L = −N 1 .. . −Nn . Odp. a = − 2 . 4847366 · 10 − 05 , b = − 8 . 4104917 · 10 − 06 , c = 29 . 7714 , m 0 = 0 . 0045 . N 200 = 29 . 5788 m. Rozwiązanie - składowe odchylenia linii pionu. Składowe ξ oraz η wyznaczymy metodą najmniejszych kwadratów zgodnie z zależnością: θij = − ∆ Nij sij = ξ cos Azij + η sin Azij, gdzie ∆ Nij oznacza różnicę odstępów między i-tym a j-tym punktem, sij od- ległość między tymi punktami, a Azij azymut boku ij . Obliczenia przepro- wadzimy dla czterech boków: 1-3, 3-4, 4-6 i 6-1. W tym przypadku macierze A i L mają postać: A = cos Azij sin Azij .. . .. . , L = ∆ Nij sij .. . . Odp. ξ = 5 . 11 , η = 1 . 70 , m 0 = 0 . 28 . Wyniki pośrednie przedstawione są w tabeli. Nr-Nr dx[m] dy[m] dN[m] Az[ ◦ ] s[m] 1-3 -3297.914 2777.874 0.064 139.892148 4311.939 3-4 -3889.563 -882.685 0.099 192.785963 3988.463 4-6 3891.744 -6377.847 -0.040 301.391422 7471.453 6-1 3295.733 4482.658 -0.123 53.675987 5563.819 9
... zobacz całą notatkę




Komentarze użytkowników (0)