To tylko jedna z 2 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
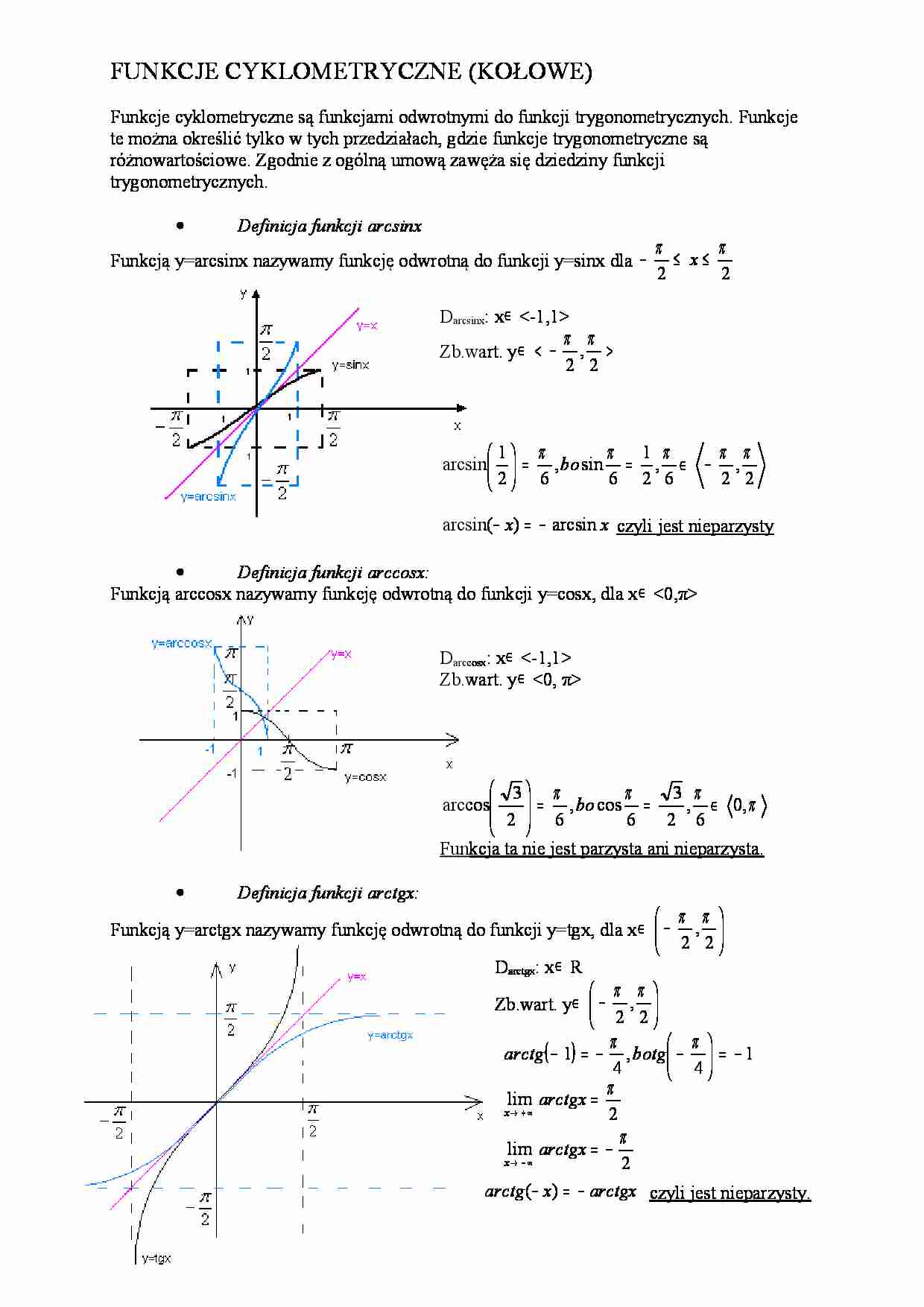

( ) 1 4 , 4 1 − = − − = − π π botg arctg 2 lim 2 lim π π − = = − ∞ → + ∞ → arctgx arctgx x x FUNKCJE CYKLOMETRYCZNE (KOŁOWE) Funkcje cyklometryczne są funkcjami odwrotnymi do funkcji trygonometrycznych. Funkcje te można określić tylko w tych przedziałach, gdzie funkcje trygonometryczne są różnowartościowe. Zgodnie z ogólną umową zawęża się dziedziny funkcji trygonometrycznych. • Definicja funkcji arcsinx Funkcją y=arcsinx nazywamy funkcję odwrotną do funkcji y=sinx dla 2 2 π π ≤ ≤ − x Darcsinx: x∈ Zb.wart. y∈ − Darccosx: x∈ Zb.wart. y∈ π π π π , 0 6 , 2 3 6 cos , 6 2 3 arccos ∈ = = bo Funkcja ta nie jest parzysta ani nieparzysta. • Definicja funkcji arctgx: Funkcją y=arctgx nazywamy funkcję odwrotną do funkcji y=tgx, dla x∈ − 2 , 2 π π Darctgx: x∈ R Zb.wart. y∈ − 2 , 2 π π arctgx x arctg − = − ) ( czyli jest nieparzysty. 1 ; 1 : . . 1 1 1 / 4 1 2 arccos 0 2 5 , 2 3 : 2 5 2 3 2 : / 5 2 3 1 / 4 1 2 4 4 / 1 4 1 2 1 1 4 1 2 arccos ) ( + ∈ + ≤ ≤ + ≤ − ≤ − ∈ ≤ ≤ − ≤ ≤ − + ≤ − ≤ − ⋅ ≤ − ≤ − + − = π π π y wart Zb y x x D x x x x x x f f 10 7 , 10 3 : . . 10 7 10 3 2 / 6 ) 2 arcsin( 2 3 , 1 : 3 1 2 / 1 2 1 2 ) 2 arcsin( 5 2 ) ( π π π π π π π π ∈ ≤ ≤ + ≤ − ≤ − ∈
(…)
… -arccosx
Przykłady:
Wyznaczyć dziedzinę i przeciwdziedzinę funkcji:
2x − 1
a)
b)
2
π
f ( x ) = arccos
+1
g ( x ) = arcsin( x − 2) +
4
5
2
2x − 1
− 1 ≤ x − 2 ≤ 1/+ 2
− 1≤
≤ 1 /⋅ 4
4
1≤ x ≤ 3
− 4 ≤ 2x − 1 ≤ 4 /+ 1
D g : x ∈ < 1,3 >
− 3 ≤ 2x ≤ 5 / : 2
π
π
π
− ≤ arcsin( x − 2) ≤ / +
3
5
− ≤ x≤
2
6
2
2
2
3π
7π
≤ y≤
3 5
Df : x ∈ − ,
10
10
2 2
3π 7π
Zb.wart. : y ∈
,
2x − 1
10 10
0 ≤ arccos
≤ π /+ 1
4
1≤ y ≤ π…
... zobacz całą notatkę




Komentarze użytkowników (0)