To tylko jedna z 3 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
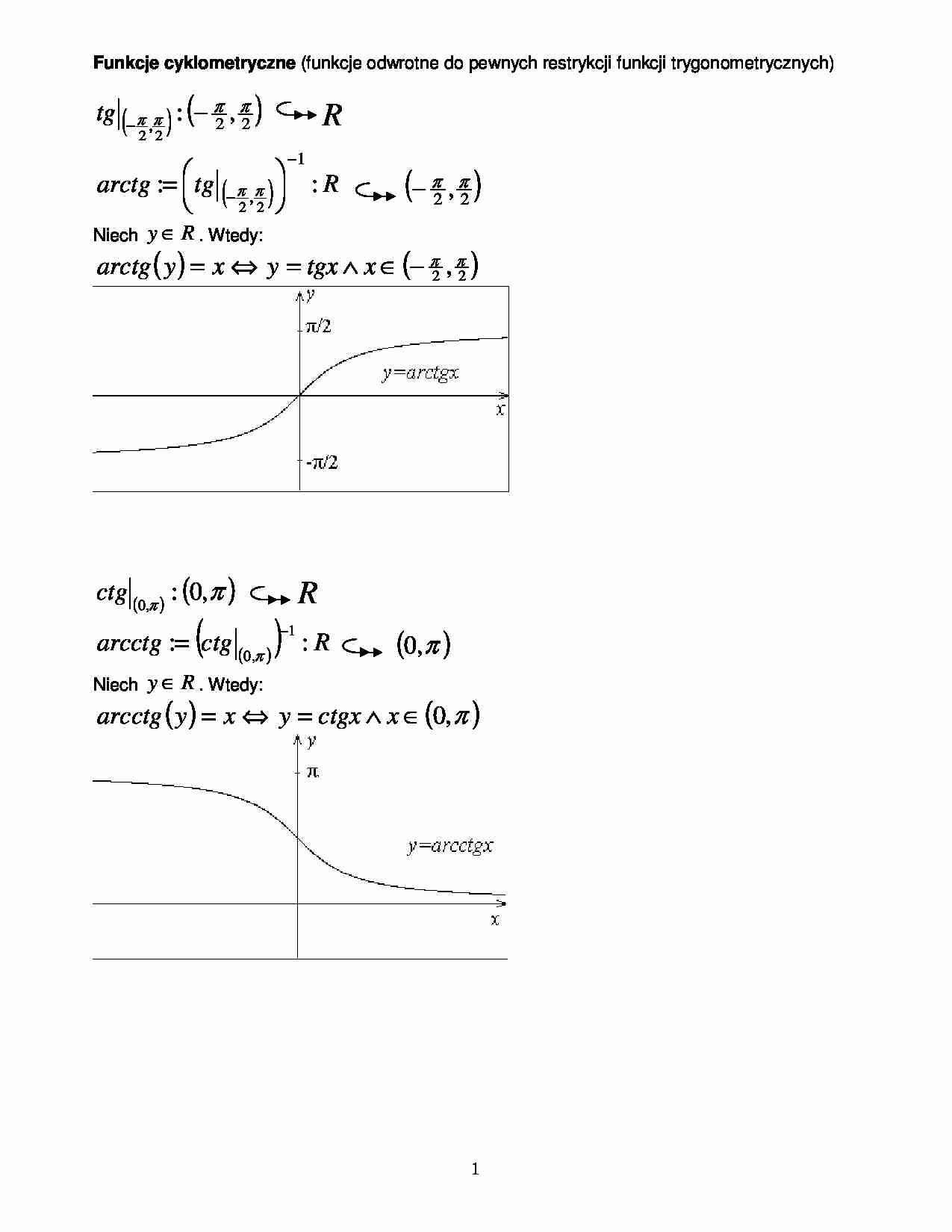


1 Funkcje cyklometryczne (funkcje odwrotne do pewnych restrykcji funkcji trygonometrycznych) ( ) ( ) 2 2 , , : 2 2 π π π π − − tg R ( ) R tg arctg : : 1 , 2 2 − − = π π ( ) 2 2 , π π − Niech R y ∈ . Wtedy: ( ) ( ) 2 2 , π π − ∈ ∧ = ⇔ = x tgx y x y arctg ( ) ( ) π π , 0 : , 0 tg c R ( ) ( ) R tg c arcctg : : 1 , 0 − = π ( ) π , 0 Niech R y ∈ . Wtedy: ( ) ( ) π , 0 ∈ ∧ = ⇔ = x ctgx y x y arcctg 2 [ ] [ ] 2 2 , , : sin 2 2 π π π π − − [ ]1, 1 − [ ] ( ) [ ]1,1 : sin : arcsin 1 , 2 2 − = − − π π [ ] 2 2 , π π − Niech [ ]1 , 1 − ∈ y . Wtedy: ( ) [ ] 2 2 , sin arcsin π π − ∈ ∧ = ⇔ = x x y x y [ ] [ ] π π , 0 : cos , 0 [ ]1, 1 − [ ] ( ) [ ]1, 1 : cos : arccos 1 , 0 − = − π [ ] π , 0 Niech [ ]1 , 1 − ∈ y . Wtedy: ( ) [ ] π , 0 cos arccos ∈ ∧ = ⇔ = x x y x y 3 Własno ci: ( ) x tgx arctg = , je li ( ) 2 2 , π π − ∈ x ( ) y arctgy tg = , je li R y ∈ ( ) x ctgx arcctg = , je li ( ) π , 0 ∈ x ( ) y arcctgy ctg = , je li R y ∈ ( ) x x = sin arcsin , je li [ ] 2 2 , π π − ∈ x ( ) y y = arcsin sin , je li [ ]1 , 1 − ∈ y ( ) x x = cos arccos , je li [ ] π , 0 ∈ x ( ) y y = arccos cos , je li [ ]1 , 1 − ∈ y
... zobacz całą notatkę






Komentarze użytkowników (0)