To tylko jedna z 3 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
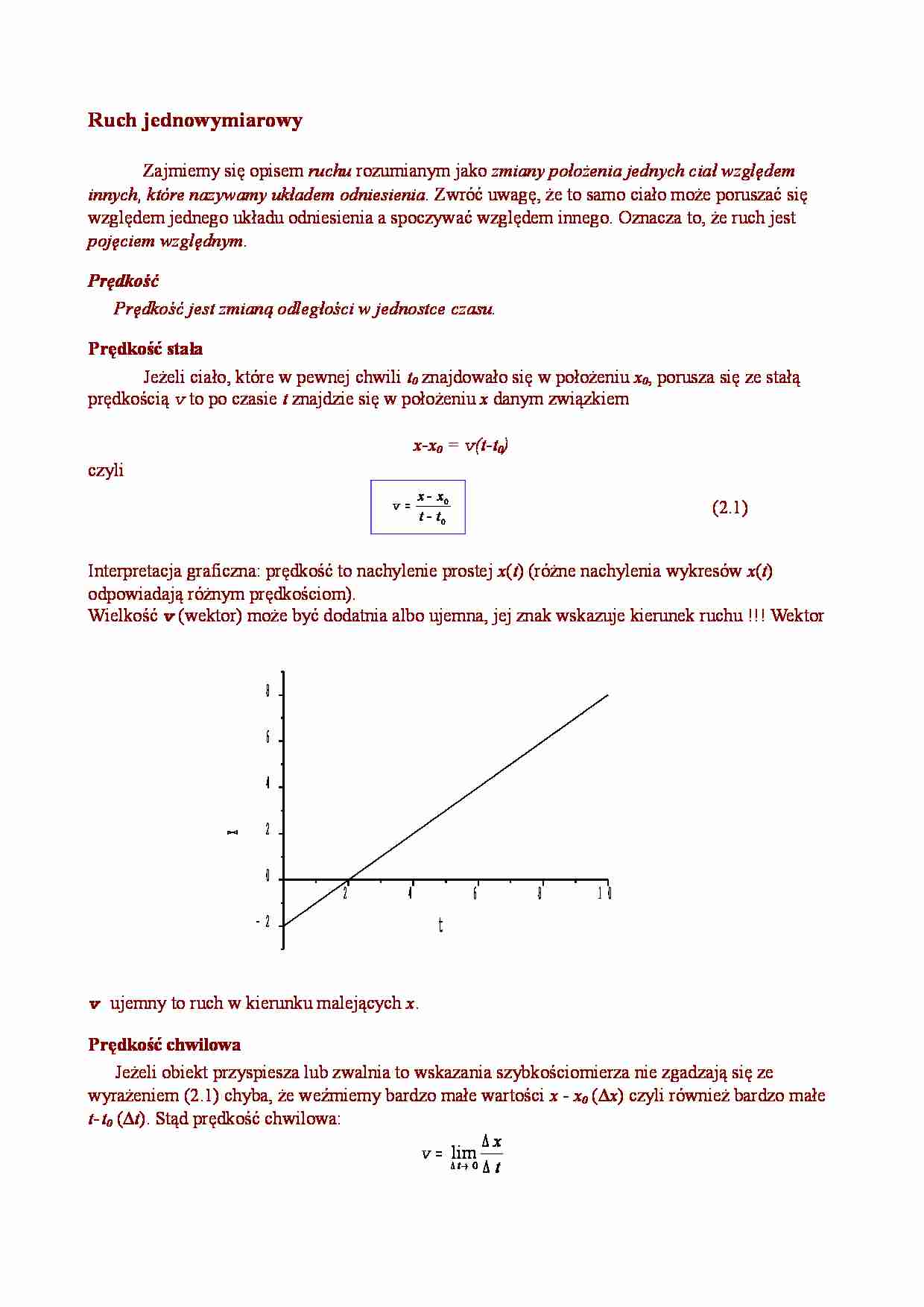


Ruch jednowymiarowy Zajmiemy się opisem ruchu rozumianym jako zmiany położenia jednych ciał względem innych, które nazywamy układem odniesienia. Zwróć uwagę, że to samo ciało może poruszać się względem jednego układu odniesienia a spoczywać względem innego. Oznacza to, że ruch jest pojęciem względnym . Prędkość Prędkość jest zmianą odległości w jednostce czasu. Prędkość stała Jeżeli ciało, które w pewnej chwili t0 znajdowało się w położeniu x0 , porusza się ze stałą prędkością v to po czasie t znajdzie się w położeniu x danym związkiem x-x0 = v(t-t0) czyli 0 0 t t x x − − = v (2.1) Interpretacja graficzna: prędkość to nachylenie prostej x ( t ) (różne nachylenia wykresów x ( t ) odpowiadają różnym prędkościom). Wielkość v (wektor) może być dodatnia albo ujemna, jej znak wskazuje kierunek ruchu !!! Wektor v ujemny to ruch w kierunku malejących x . Prędkość chwilowa Jeżeli obiekt przyspiesza lub zwalnia to wskazania szybkościomierza nie zgadzają się ze wyrażeniem (2.1) chyba, że weźmiemy bardzo małe wartości x - x0 ( ∆ x ) czyli również bardzo małe t-t0 ( ∆ t ). Stąd prędkość chwilowa: t x t ∆ ∆ = → ∆ 0 lim v 2 4 6 8 1 0 - 2 0 2 4 6 8 x t Tak definiuje się pierwszą pochodną, więc t d d x = v (2.2) Prezentacja graficzna Prędkość chwilowa przejście od siecznej do stycznej. Nachylenie stycznej to prędkość chwilowa (w chwili t odpowiadającej punktowi styczności). Prędkość średnia Średnia matematyczna. Znaczenie średniej - przykłady. Przykłady rozkładów niejednostajnych - czynniki wagowe. Przyspieszenie Przyspieszenie to tempo zmian prędkości. Przyspieszenie jednostajne i chwilowe Prędkość zmienia się jednostajnie z czasem czyli przyspieszenie t 0 v v − = a (2.4) jest stałe . Gdy przyspieszenie zmienia się z czasem musimy wtedy ograniczyć się do pomiaru zmian prędkości ∆ v w bardzo krótkim czasie ∆ t (analogicznie do prędkości chwilowej). Odpowiada to pierwszej pochodnej v względem t . t d d v = a (2.5) Ruch jednostajnie zmienny Często chcemy znać zarówno położenie ciała i jego prędkość. Ze wzoru (2.4) mamy 0 2 4 6 0 20 40 60 80 x t v = v0 + at . Natomiast do policzenia położenia skorzystamy ze wzoru (2.3). t x x v + = 0 Ponieważ w ruchu jednostajnie przyspieszonym prędkość rośnie jednostajnie od v 0 do v więc prędkość średnia wynosi v = ( v 0 + v )/2 Łącząc otrzymujemy
... zobacz całą notatkę






Komentarze użytkowników (0)