To tylko jedna z 3 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


3.2. Drzewa rozbioru syntaktycznego
Drzewo rozbioru syntaktycznego według gramatyki G = ∈GBK jest to drzewo
zorientowane z korzeniem k0 i funkcją etykietującą wierzchołki f: K!M, jeśli
spełnione są następujące warunki:
k0
(1) M ⊆ (N ∪ T) ∪{ε}
(2) f(k0) = Z
... kn
k2
k1
(3) niech k1,...,kn będą bezpośrednimi potomkami korzenia k0;
wówczas: (Z → f(k1)f(k2)...f(kn)) ∈ P
(4) jeśli f(ki) ∈ T lub jeśli n = 1 i f(ki) = ε, to ki jest liściem
(5) jeśli f(ki) ∈ N, to ki jest korzeniem drzewa (poddrzewa) rozbioru według gramatyki
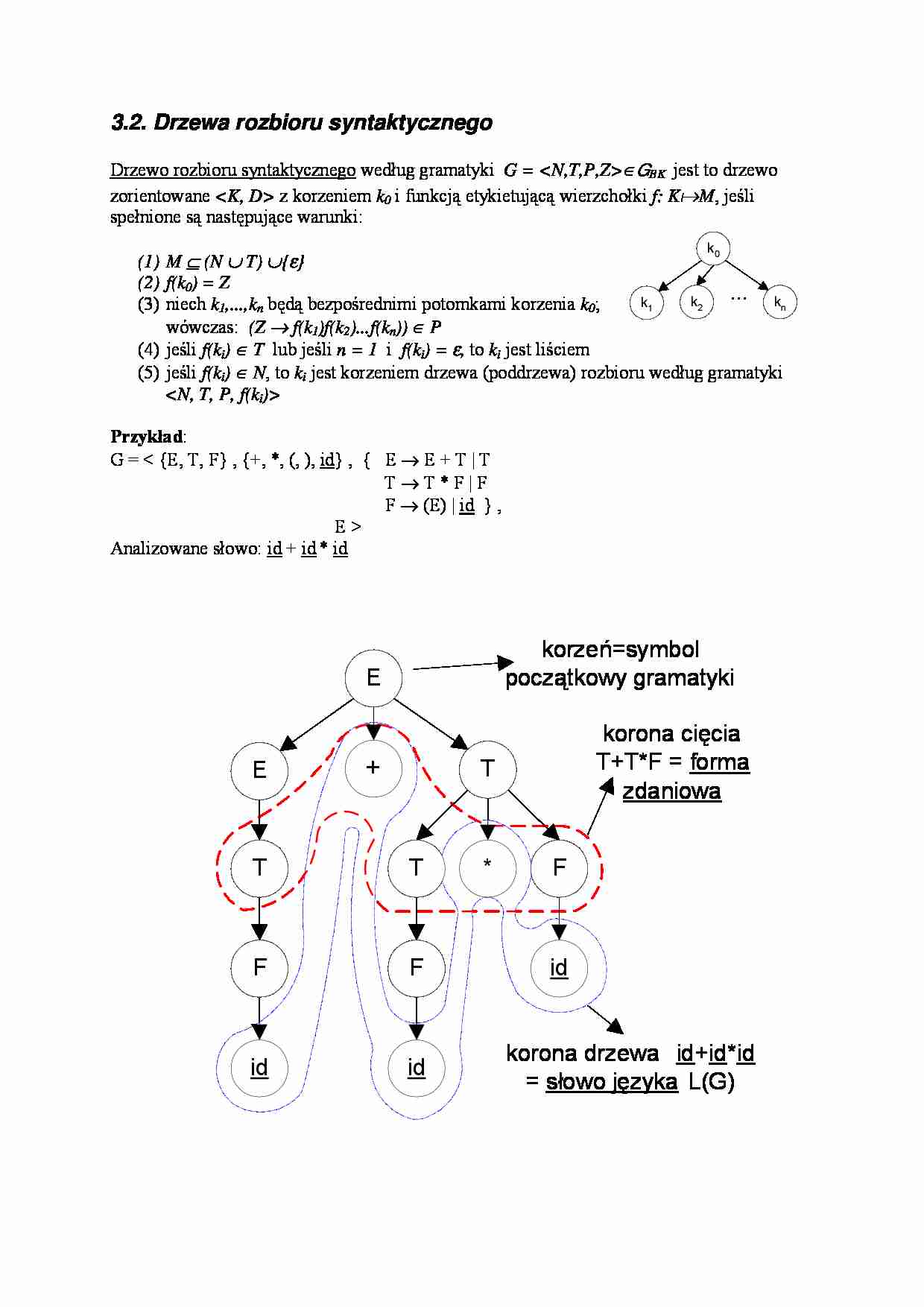
Przykład:
G =
Analizowane słowo: id + id * id
korzeń=symbol
początkowy gramatyki
E
E
+
korona cięcia
T+T*F = forma
zdaniowa
T
T
T
F
F
id
id
*
F
id
korona drzewa id+id*id
= słowo języka L(G)
E
poddrzewo o korzeniu T
E
+
T
T
T
F
F
id
id
F
*
korona cięcia T*F
poddrzewa tworzy frazę
związaną z korzeniem
poddrzewa T T*F
jest frazą formy T+T*F
dla T
id
G =
Analizowane słowo: id + id * id
Wyprowadzanie
lewostronne
Drzewo rozbioru
syntaktycznego
E
E
E+T
T+T
F+T
id+T
id+T*F
id+F*F
id+id*F
id+id*id
Wyprowadzanie
prawostronne
E
E+T
E+T*F
E+T*id
E+F*id
E+id*id
T+id*id
F+id*id
id+id*id
E
+
T
T
T * F
F
F
id
id
id
Przykład:
G =
Analizowane słowo: id + id * id
E
E
id
E
+
E
E
E * E
id
id
*
E + E
id
E
id
id
Dla pewnego słowa (u nas: id + id * id) udało się zbudować dwa różne drzewa rozbioru
syntaktycznego. Taka gramatyka jest niejednoznaczna.
Podsumowanie:
- Dla każdego drzewa rozbioru syntaktycznego istnieje co najmniej jedno wyprowadzenie
słowa języka L(G) w gramatyce G
- Dla każdego wyprowadzenia słowa istnieje odpowiadające mu drzewo rozbioru
syntaktycznego. Kilku różnym wyprowadzeniom mogą odpowiadać identyczne drzewa
rozbioru syntaktycznego.
- Dwa wyprowadzenia są równoważne, gdy odpowiadające im drzewa rozbioru
syntaktycznego są identyczne.
- Słowo języka L(G) jest niejednoznaczne w gramatyce G, jeśli jego wyprowadzenia można
opisać przez co najmniej dwa różne drzewa rozbioru syntaktycznego
- Gramatyka G jest niejednoznaczna, jeśli w języku L(G) istnieje co najmniej jedno
niejednoznaczne słowo w tej gramatyce. W przeciwnym wypadku gramatyka jest
jednoznaczna. W gramatyce jednoznacznej istnieje dokładnie jedno wyprowadzenie
lewostronne i dokładnie jedno wyprowadzenie prawostronne (wśród wszystkich
równoważnych wyprowadzeń tego samego słowa)
... zobacz całą notatkę






Komentarze użytkowników (0)