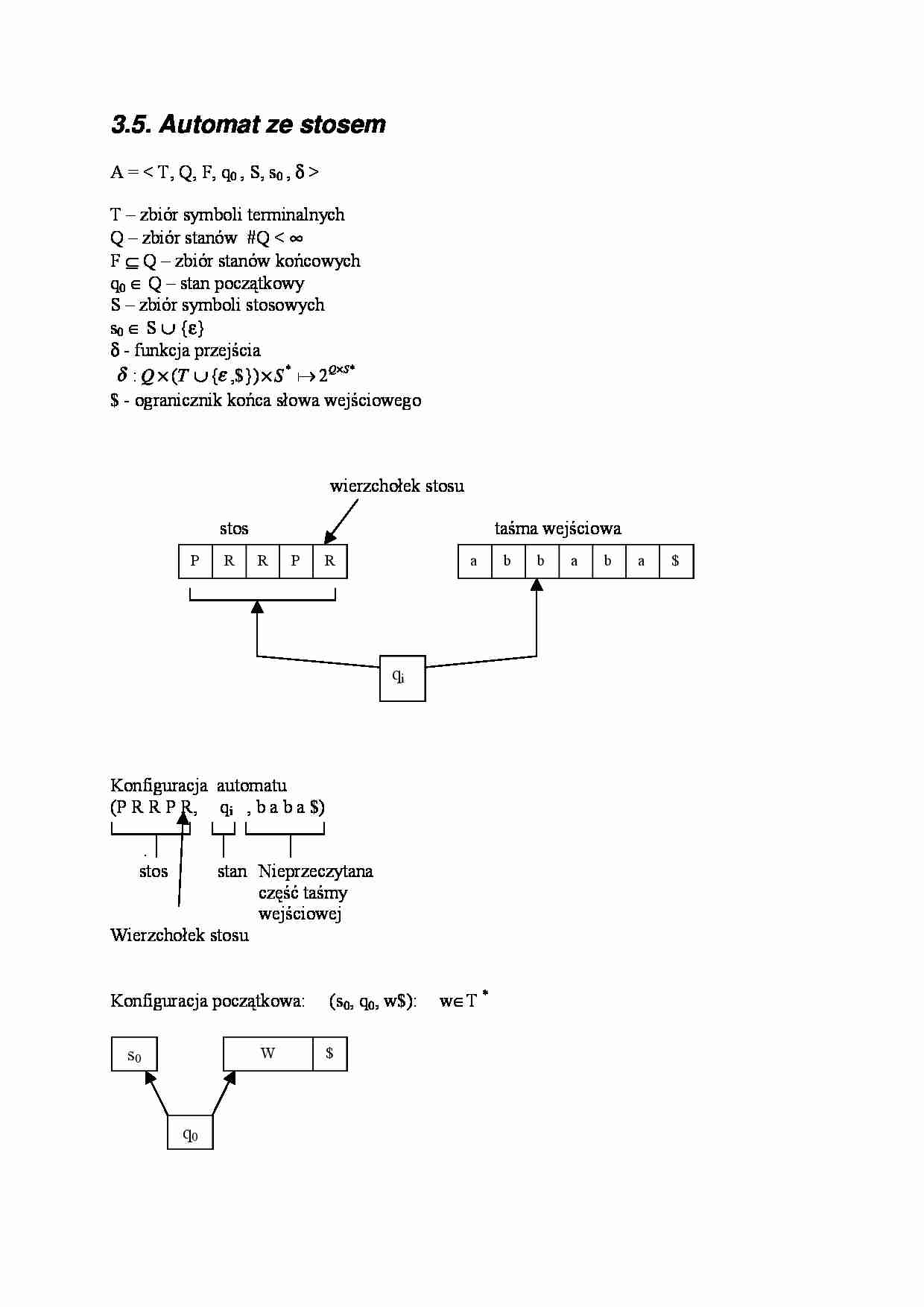
3.5. Automat ze stosem
A =
T – zbiór symboli terminalnych
Q – zbiór stanów #Q
T = { 0, 1}
G = ∈ GBK
Q = { q0, q1, q2}; F = {q0}
N = {Z}
q0 – stan początkowy
T = { 0 , 1}
S = {R, 0 }
P = {Z → 0Z1 | ε }
s0 = R
(1) δ (q0, 0, R} ={(q1, R0 )}
(2) δ (q1, 0, 0} ={(q1, 00 )}
(3) δ (q1, 1, 0} ={(q2, ε )}
(4) δ (q2, 1, 0} ={(q2, ε )}
(5) δ (q2, $, R} ={(q0, ε )}
(6) δ (q0, $, R} ={(q0, ε )}
Analizowane
000111$
słowo:
(R, q0, 000111$ )
" (R0, q1, 00111$)
(2)
" (R00, q1, 0111$)
(2)
" (R000, q1, 111$)
(3)
" (R00, q2, 11$)
(4)
" (R0, q2, 1$)
(4)
" (R, q2, $)
(5)
" ( ε, q0, $)
(1)
x ∈ T* jest słowem akceptowanym przez automat A (ze stosem) ⇔
( ∃q ∈ F ) ( (s0 , q0, x$) "A* ( ε, q, $) )
Język L jest akceptowany przez automat A (co oznaczamy L(A)) ⇔
L = L(A) = {x ∈ T* | x jest akceptowane przez A}
Tw. Dla każdej gramatyki bezkontekstowej G ∈ GBK istnieje automat ze stosem A, taki, że
L(A) = L(G)
Def. Odbiciem zwierciadlanym (rewersem) słowa x ∈ V* gdzie x = x1 x2... xn, xi ∈ V jest
słowo xR = xnxn-1...x2x1
Konstrukcja automatu ze stosem odtwarzającego wywód lewostronny w gramatyce G ∈ GBK
(top - down)
We: G = ∈ GBK
Wy: A =
taki, że L(A) = L(G)
Rozwiązanie
Q : = {q};
F: = {q};
q0: = q;
S := N∩T;
s0: = Z;
for (A→x) ∈ P do
do δ (q, ε, A) włącz (q, xR);
for a ∈ T do
do δ (q, a, a) włącz (q, ε);
Przykład:
G =
A =
δ (q, ε , E} ={(1)(q, T+ F ), (2)(q, T)}
δ (q, ε , T} ={(3)(q, F*T ), (4)(q, F)}
δ (q, ε , F} ={(5)(q, )E( ), (6)(q, id )}
δ (q, b , b} ={(pop)(q, ε)} dla wszystkich b ∈ { id, +, *, ( , )}
(1)
"
(2)
"
" (4)
(6)
"
(pop)
"
(pop)
"
(3)
"
... zobacz całą notatkę





Komentarze użytkowników (0)