To tylko jedna z 9 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
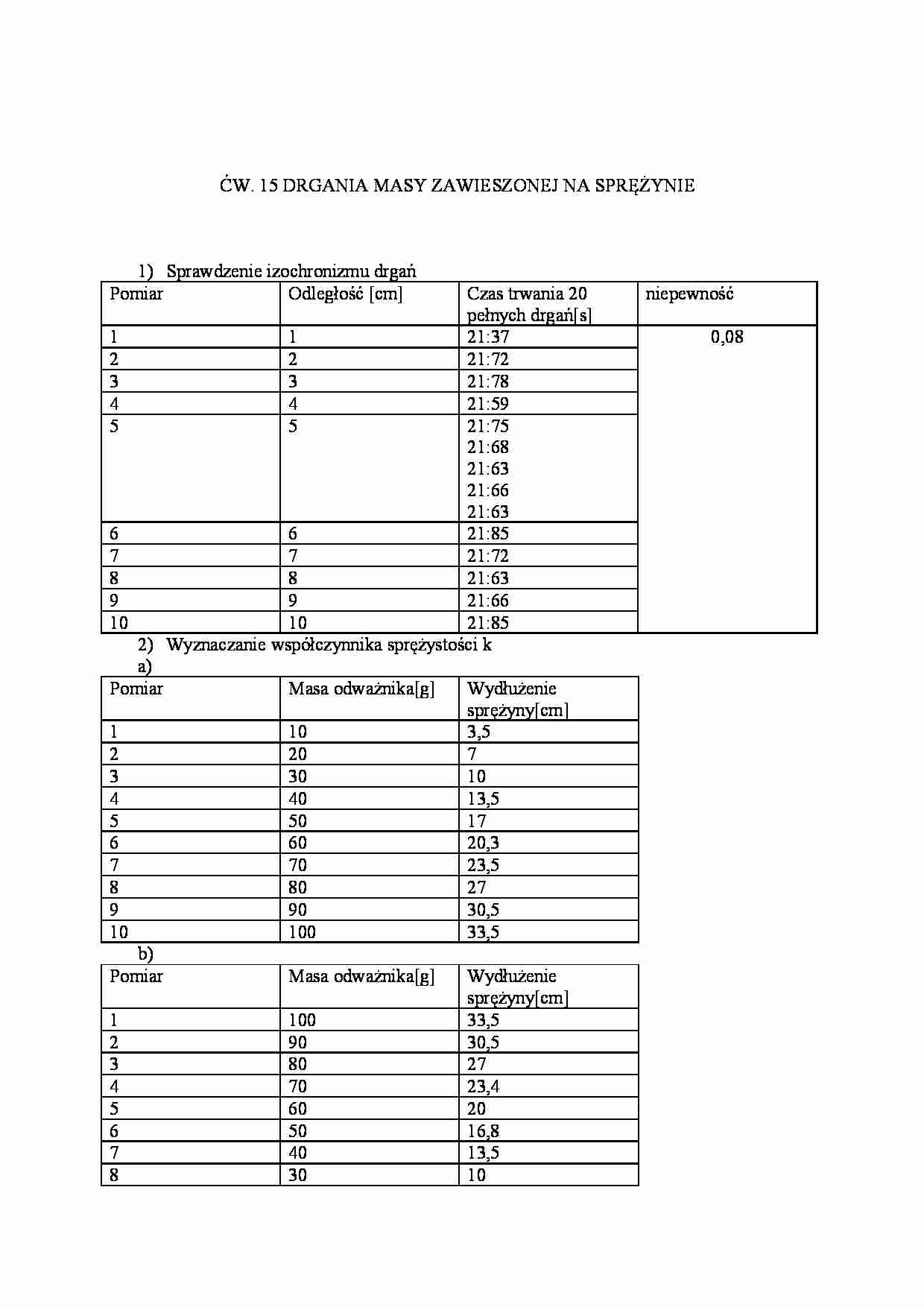


ĆW. 15 DRGANIA MASY ZAWIESZONEJ NA SPRĘŻYNIE 1) Sprawdzenie izochronizmu drgań Pomiar Odległość [cm] Czas trwania 20 pełnych drgań[s] niepewność 1 1 21:37 0,08 2 2 21:72 3 3 21:78 4 4 21:59 5 5 21:75 21:68 21:63 21:66 21:63 6 6 21:85 7 7 21:72 8 8 21:63 9 9 21:66 10 10 21:85 2) Wyznaczanie współczynnika sprężystości k a) Pomiar Masa odważnika[g] Wydłużenie sprężyny[cm] 1 10 3,5 2 20 7 3 30 10 4 40 13,5 5 50 17 6 60 20,3 7 70 23,5 8 80 27 9 90 30,5 10 100 33,5 b) Pomiar Masa odważnika[g] Wydłużenie sprężyny[cm] 1 100 33,5 2 90 30,5 3 80 27 4 70 23,4 5 60 20 6 50 16,8 7 40 13,5 8 30 10 9 20 6,7 10 10 3,2 3) pomiar Odległość [cm] Masa odważnika[g] 40 50 60 70 80 90 100 nieznana Czas trwania 20 pełnych drgań[s] 1 1 20:59 21:50 22:66 23:78 24:78 25:72 26:68 21:86 2 2 20:47 21:75 22:63 23:85 24:94 25:82 26:85 21:82 3 3 20:59 21:68 22:72 23:87 24:66 25:78 26:78 21:94 4 4 20:59 21:78 22:87 23:59 24:59 25:94 21:41 5 5 20:87 21:53 22:87 23:97 24:91 25:68 21:63 6 6 20:50 21:72 22:82 23:85 24:78 25:78 21:72 7 7 20:53 21:78 22:97 23:66 24:82 21:78 8 8 20:50 21:82 22:37 23:87 24:75 21:94 9 9 20:41 21:66 2:78 23:85 24:28 21:82 10 10 20:66 21:68 22:82 23:72 24:72 21:68 Opis teoretyczny: Siły sprężyste- są one związane ze sprężystym odkształceniem ciał pod wpływem siły zewnętrznej. Odkształcenia te powodują siły sprężystości równoważące siły zewnętrzne, które pojawiają się w odkształconym ciele. Np. Na rysunku tym siła zewnętrzna 2 F działającą na zamocowaną za jeden koniec sprężynę wywołuje powstanie siły sprężystości 2 5 F F . W pewnym zakresie odkształceń odkształcenie sprężyste jest wprost proporcjonalne do wywołującej je siły. Prawo Hooke’a- prawo to mówi, że dla niewielkich odkształceń, odkształcenie ciała jest proporcjonalne do przyłożonego naprężenia: F=-kx Gdzie: x- wydłużenie sprężyny równe jest wychyleniu punktu drgającego k- współczynnik proporcjonalności natomiast znak „-‘’ oznacza że siła F ma kierunek odwrotny niż wychylenie x. Jeśli przekształcimy wzór otrzymujemy: x F k Prawo Hooke’a mówi również, iż naprężenie wewnętrzne ciała jest wprost proporcjonalne do jego wydłużenia względnego: 0 l l E p Gdzie: E- moduł sprężystości Younga. Moduł ten odpowiada takiemu wydłużeniu, przy którym materiał uległby dwukrotnemu wydłużeniu , gdyby wcześniej nie uległ zerwaniu.
(…)
… przyspieszonym
zgodnie z II zasadą dynamiki Newtona, jeśli sprężyna wydłuży się tak, aby wypadkowa
ciężaru(mg) i siły sprężystej(kx), działających na masę m nie była równa 0:
d2x
a
dt 2
Natomiast równanie ruchu ma postać:
d 2x
m 2 mg kx
dt
mg
Po dalszych przekształceniach oraz po podstawieniu zależności x 0
k
Otrzymujemy postać:
d 2x k
( x x0 ) 0
dt 2 m
Po wprowadzeniu wychylenia masy m z położenia…
... zobacz całą notatkę






Komentarze użytkowników (0)