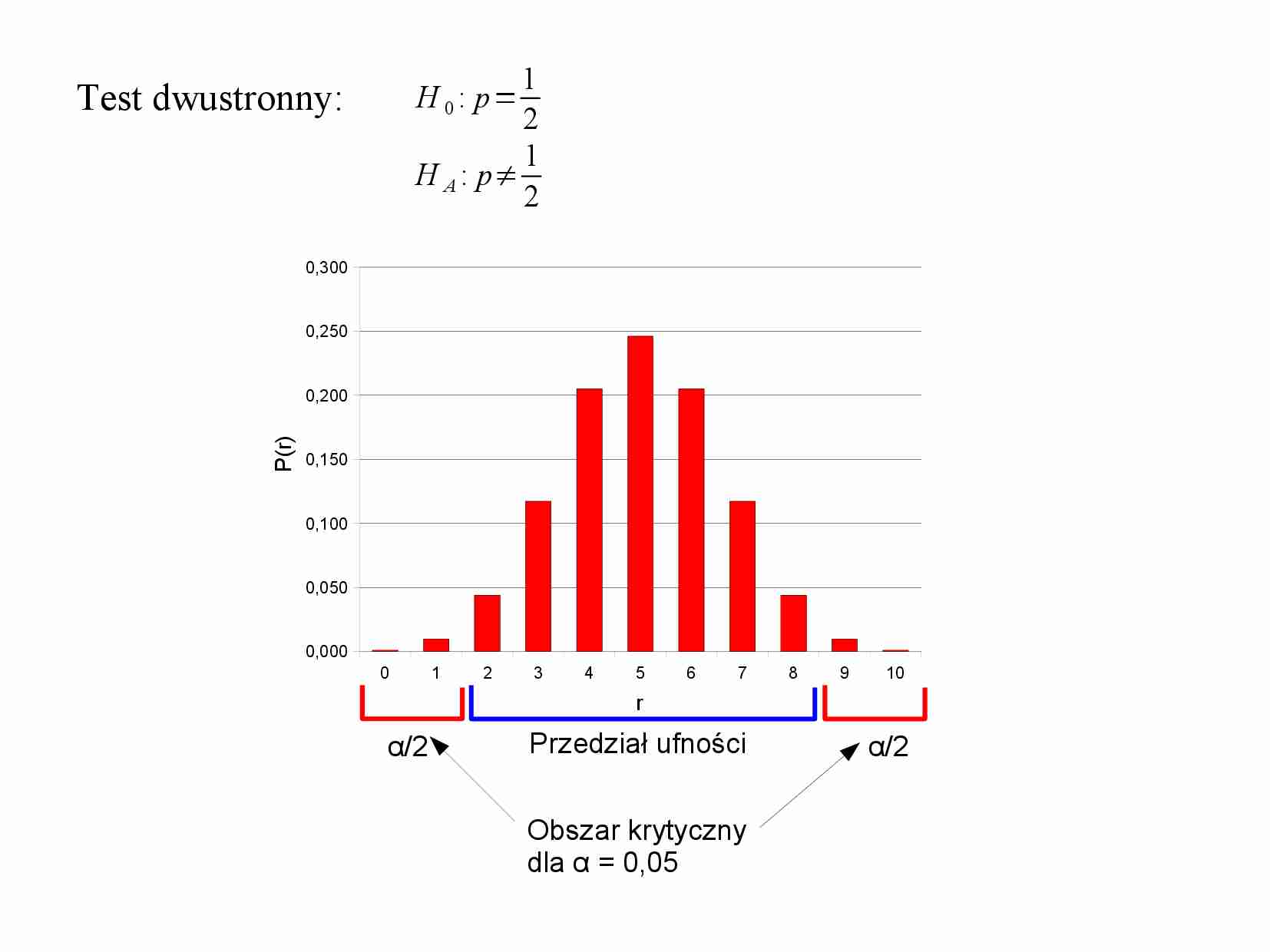
0 1 2 3 4 5 6 7 8 9 10 0,000 0,050 0,100 0,150 0,200 0,250 0,300 r P (r ) Przedział ufności Obszar krytyczny dla α = 0,05 α/2 α/2 Test dwustronny: H 0 : p = 1 2 H A : p ≠ 1 2 Prawo Murphy'ego : kanapka zazwyczaj spada posmarowaną stroną do dołu. Zrzucono 10 razy kanapkę na dywan. 8 razy kanapka spadła posmarowaną stroną do dołu. Czy można uznać, że prawo Murphy'ego jest prawdziwe? Przetestuj hipotezę dla poziomu istotności α = 0,05 i α = 0,1. α = 0,05 0 1 2 3 4 5 6 7 8 9 10 0,000 0,050 0,100 0,150 0,200 0,250 0,300 r P (r ) Przedział ufności Obszar krytyczny dla α = 0,05 α P (r=0) = 1/1024 P (r=1) = 10/1024 P (r=2) = 45/1024 P (r=3) = 120/1024 P (r=4) = 210/1024 P (r=5) = 252/1024 P (r=6) = 210/1024 P (r=7) = 120/1024 P (r=8) = 45/1024 P (r=9) = 10/1024 P (r=10) = 1/1024 p = 56/1024 = 5,5% α = 0,1 0 1 2 3 4 5 6 7 8 9 10 0,000 0,050 0,100 0,150 0,200 0,250 0,300 r P (r ) Przedział ufności Obszar krytyczny dla α = 0,1 α P (r=0) = 1/1024 P (r=1) = 10/1024 P (r=2) = 45/1024 P (r=3) = 120/1024 P (r=4) = 210/1024 P (r=5) = 252/1024 P (r=6) = 210/1024 P (r=7) = 120/1024 P (r=8) = 45/1024 P (r=9) = 10/1024 P (r=10) = 1/1024 p = 56/1024 = 5,5% Zadanie: Jakie jest prawdopodobieństwo, że uda się zidentyfikować krzywą monetę (p=0,3) przy dziesięciu rzutach monetą? Wyznaczamy obszar krytyczny i przedział ufności dla n = 10. Przyjmujemy poziom istotności testu α = 0,05. P (r=0) = 1/1024 P (r=1) = 10/1024 P (r=2) = 45/1024 P (r=3) = 120/1024 P (r=4) = 210/1024 P (r=5) = 252/1024 P (r=6) = 210/1024 P (r=7) = 120/1024 P (r=8) = 45/1024 P (r=9) = 10/1024 P (r=10) = 1/1024 0 1 2 3 4 5 6 7 8 9 10 0,000 0,050 0,100 0,150 0,200 0,250 0,300 r P (r ) Przedział ufności Obszar krytyczny dla α = 0,05 α/2 α/2 p = 22/1024 = 2,1% 0 1 2 3 4 5 6 7 8 9 10 0,00 0,05 0,10 0,15 0,20 0,25 0,30 p=0.5 p=0.3 r P (r ) Zadanie: Jakie jest prawdopodobieństwo, że uda się zidentyfikować krzywą monetę (p=0,3) przy n = 10? P (p = 0,3; r=0) = 0,028 P (p = 0,3; r=1) = 0,121 P (p = 0,3; r=2) = 0,233 P (p = 0,3; r=3) = 0,267 P (p = 0,3; r=4) = 0,200 P (p = 0,3; r=5) = 0,103 P (p = 0,3; r=6) = 0,037 P (p = 0,3; r=7) = 0,009 P (p = 0,3; r=8) = 0,001 P (p = 0,3; r=9) = 0 P (p = 0,3; r=10) = 0
(…)
….
●
Rozkład przy kodowaniu przesuwa się na skali, zwęża lub
rozszerza, ale jego zasadniczy kształt nie zmienia się.
Transformowanie danych
●
Pierwiastkowanie, podnoszenie do potęgi, obliczanie
odwrotności, logarytmowanie i antylogarytmowanie, stosowanie
funkcji trygonometrycznych,
●
Transformowanie danych stosujemy, gdy mamy do czynienia z
przypadkami zależności nieliniowych (występujących w
przyrodzie).
Np…
... zobacz całą notatkę





Komentarze użytkowników (0)