To tylko jedna z 2 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
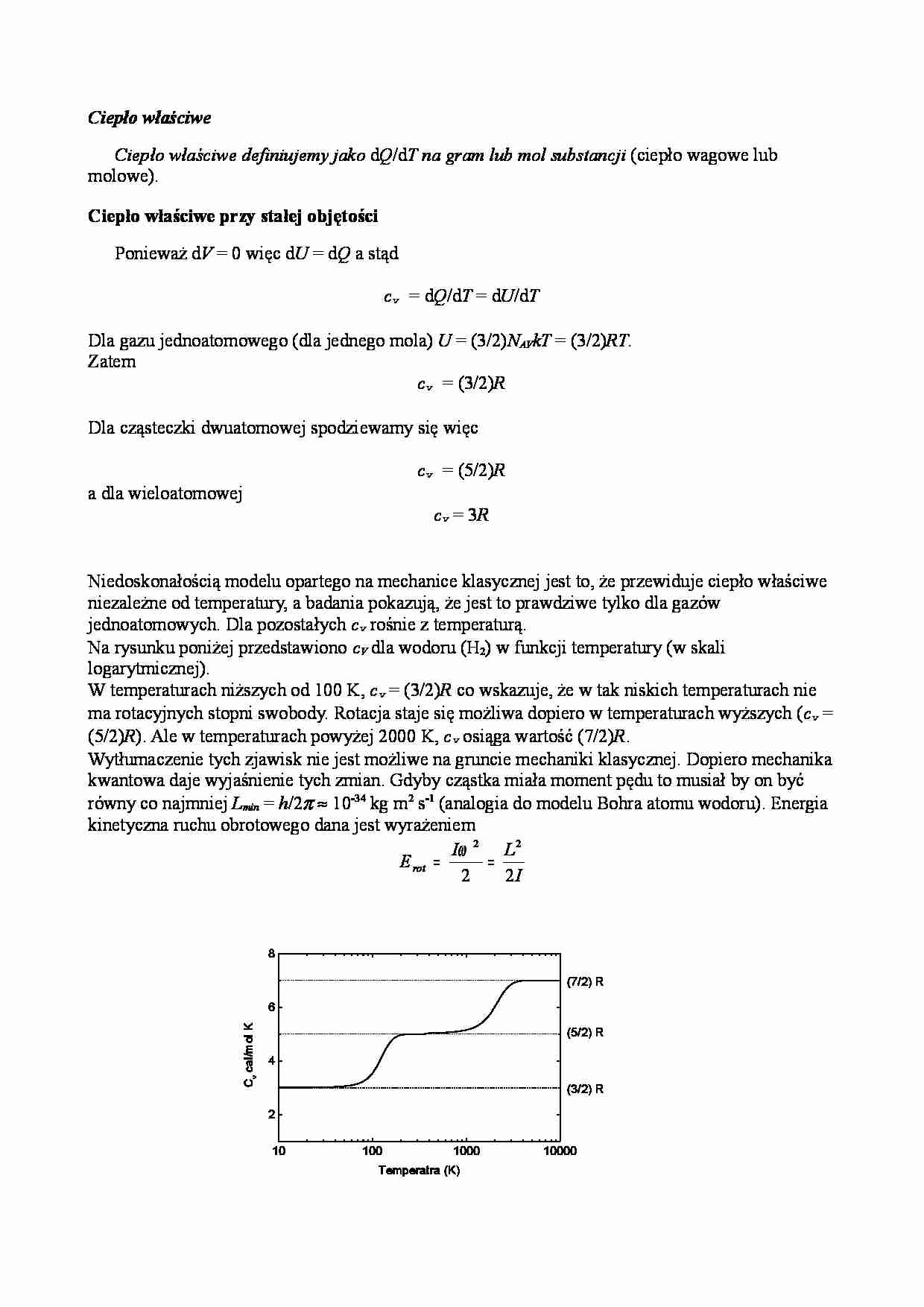

Ciepło właściwe Ciepło właściwe definiujemy jako d Q /d T na gram lub mol substancji (ciepło wagowe lub molowe). Ciepło właściwe przy stałej objętości Ponieważ d V = 0 więc d U = d Q a stąd c v = d Q /d T = d U /d T Dla gazu jednoatomowego (dla jednego mola) U = (3/2) NAVkT = (3/2) RT . Zatem c v = (3/2) R Dla cząsteczki dwuatomowej spodziewamy się więc c v = (5/2) R a dla wieloatomowej c v = 3 R Niedoskonałością modelu opartego na mechanice klasycznej jest to, że przewiduje ciepło właściwe niezależne od temperatury, a badania pokazują, że jest to prawdziwe tylko dla gazów jednoatomowych. Dla pozostałych c v rośnie z temperaturą. Na rysunku poniżej przedstawiono cV dla wodoru (H2) w funkcji temperatury (w skali logarytmicznej). W temperaturach niższych od 100 K, c v = (3/2) R co wskazuje, że w tak niskich temperaturach nie ma rotacyjnych stopni swobody. Rotacja staje się możliwa dopiero w temperaturach wyższych ( c v = (5/2) R ). Ale w temperaturach powyżej 2000 K, c v osiąga wartość (7/2) R . Wytłumaczenie tych zjawisk nie jest możliwe na gruncie mechaniki klasycznej. Dopiero mechanika kwantowa daje wyjaśnienie tych zmian. Gdyby cząstka miała moment pędu to musiał by on być równy co najmniej Lmin = h /2 π ≈ 10-34 kg m2 s-1 (analogia do modelu Bohra atomu wodoru). Energia kinetyczna ruchu obrotowego dana jest wyrażeniem I L I E rot 2 2 2 2 = = ω 10 100 1000 10000 2 4 6 8 (3/2) R (5/2) R (7/2) R C v c a l/m o l K Temperatra (K) Dla cząsteczki H2 m =1.67·10-27 kg a R ≈ 5·10-11 m, więc I = 2 mR 2 ≈ 8.3·10-48 kg m2. Ponieważ na jeden stopień swobody przypada energia kT /2 więc kT /2 = L 2/2 I czyli T = L 2/ kI Stąd dla Lmin otrzymujemy Tmin ≈ 90 K. Dla niższych temperatur energia jest za mała aby wzbudzić rotacje co wymaga pewnej minimalnej energii. Podobnie jest dla ruchu drgającego, który także jest skwantowany. Edrg,min = hv . Dla typowej cząsteczkowej częstotliwości drgań 1014 Hz (zakres widzialny) otrzymujemy energię drgań ≈ 6·10-20 J co odpowiada temperaturze około 4000 K. Tak więc z zasady ekwipartycji energii wynika, że w tak wysokich temperaturach średnia energia drgań Edrg = kT /2. Oprócz energii kinetycznej tego ruchu istnieje jeszcze jego energia potencjalna. Zatem średnia energia wewnętrzna na cząsteczkę wynosi U = Eśr,kin,post + Eśr,kin,rot + Eśr,kin,drg + Eśr,pot,drg U = (3/2) kT + (2/2) kT + (1/2) kT + (1/2) kT = (7/2) kT Dla 1 mola
... zobacz całą notatkę




Komentarze użytkowników (0)