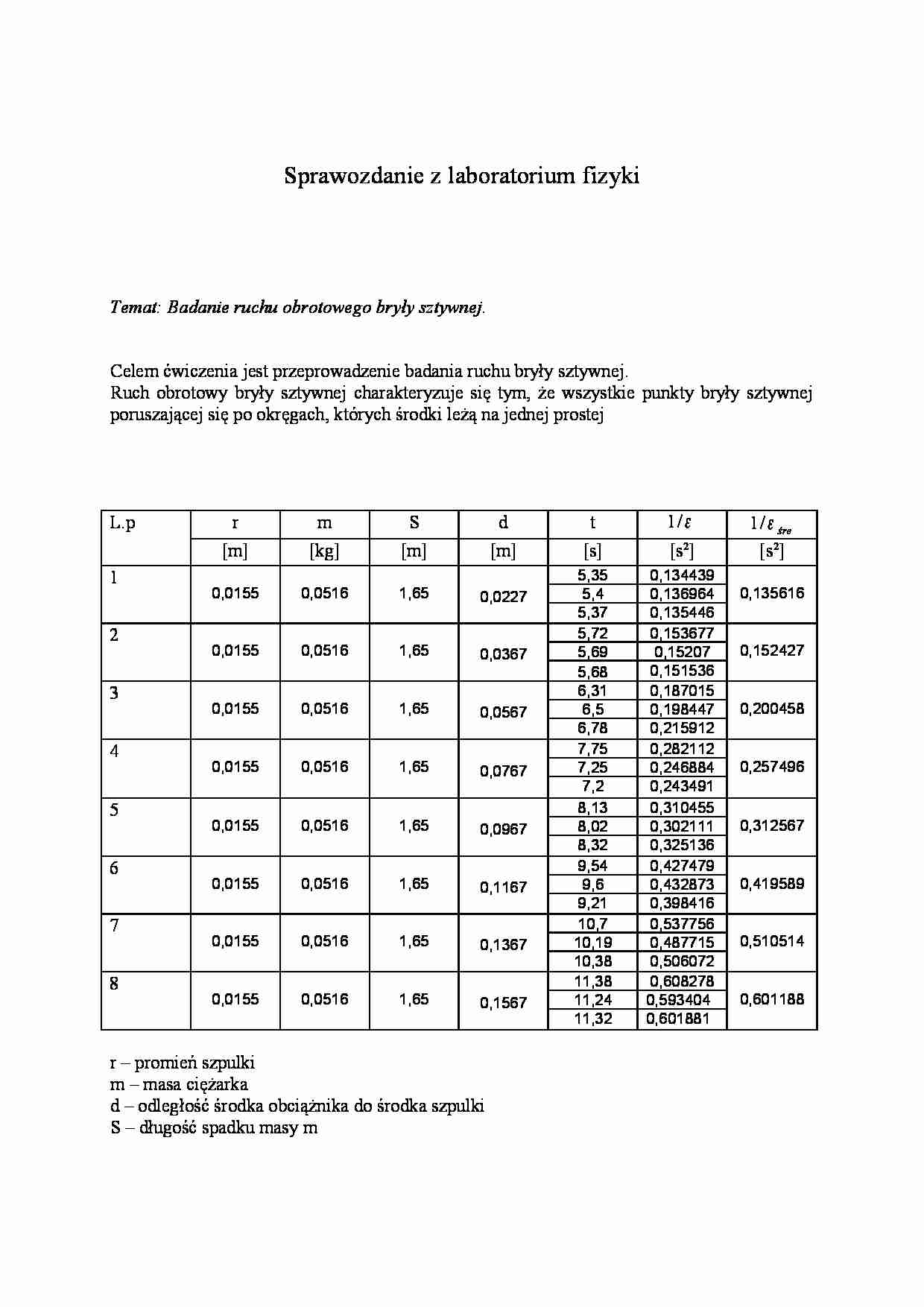
Sprawozdanie z laboratorium fizyki Temat: Badanie ruchu obrotowego bryły sztywnej. Celem ćwiczenia jest przeprowadzenie badania ruchu bryły sztywnej. Ruch obrotowy bryły sztywnej charakteryzuje się tym, że wszystkie punkty bryły sztywnej poruszającej się po okręgach, których środki leżą na jednej prostej L.p r m S d t ε / 1 śre ε / 1 [m] [kg] [m] [m] [s] [s2] [s2] 1 0,0155 0,0516 1,65 0,0227 5,35 0,134439 0,135616 5,4 0,136964 5,37 0,135446 2 0,0155 0,0516 1,65 0,0367 5,72 0,153677 0,152427 5,69 0,15207 5,68 0,151536 3 0,0155 0,0516 1,65 0,0567 6,31 0,187015 0,200458 6,5 0,198447 6,78 0,215912 4 0,0155 0,0516 1,65 0,0767 7,75 0,282112 0,257496 7,25 0,246884 7,2 0,243491 5 0,0155 0,0516 1,65 0,0967 8,13 0,310455 0,312567 8,02 0,302111 8,32 0,325136 6 0,0155 0,0516 1,65 0,1167 9,54 0,427479 0,419589 9,6 0,432873 9,21 0,398416 7 0,0155 0,0516 1,65 0,1367 10,7 0,537756 0,510514 10,19 0,487715 10,38 0,506072 8 0,0155 0,0516 1,65 0,1567 11,38 0,608278 0,601188 11,24 0,593404 11,32 0,601881 r – promień szpulki m – masa ciężarka d – odległość środka obciążnika do środka szpulki S – długość spadku masy m Przykładowe obliczenia: Obliczenia odwrotność przyspieszenia kątowego ε / 1 wykonałem ze wzoru: (wzór ćw. Laboratoryjne z fizyki) [ ]2 2 2 1 s S rt = ε Na podstawie tabeli wykreśliłem wykres ) ( 1 2 d f = ε Odczytałem z wykresu wartość odczyt ε 1 dla zerowej wartości odległości d i na tej podstawie obliczyłem moment bezwładności samego krzyżaka: M I odczyt k ⋅ = ε 1 gdzie M = mgr 135 , 0 1 = odczyt ε stąd 2 00106 , 0 m kg I k ⋅ = Błędy bezwzględne ε 1 ∆ obliczam ze wzoru: ∆ ⋅ ⋅ + ∆ ⋅ ⋅ + ∆ ⋅ ± = ∆ S S t r t S t r r S t ln 2 2 1 2 2 ε m S s t m r 001 , 0 01 , 0 0001 , 0 = ∆ = ∆ = ∆ ε 1 1 ∆ [s2] ε 1 2 ∆ [s2] ε 1 3 ∆ [s2] ε 1 średnie ∆ [s2] 0,002975 0,003026 0,002995 0,002999 0,003364 0,003331 0,00332 0,003338 0,004032 0,00426 0,004608 0,0043 0,005916 0,005221 0,005154 0,005431 0,006473 0,006309 0,006761 0,006515 0,008758 0,008863 0,008192 0,008604 0,010895 0,009927 0,010282 0,010368 0,012256 0,011969 0,012132 0,012119 Obliczam moment bezwładności wahadła Oberbecka ze wzoru:
... zobacz całą notatkę





Komentarze użytkowników (0)