To tylko jedna z 25 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
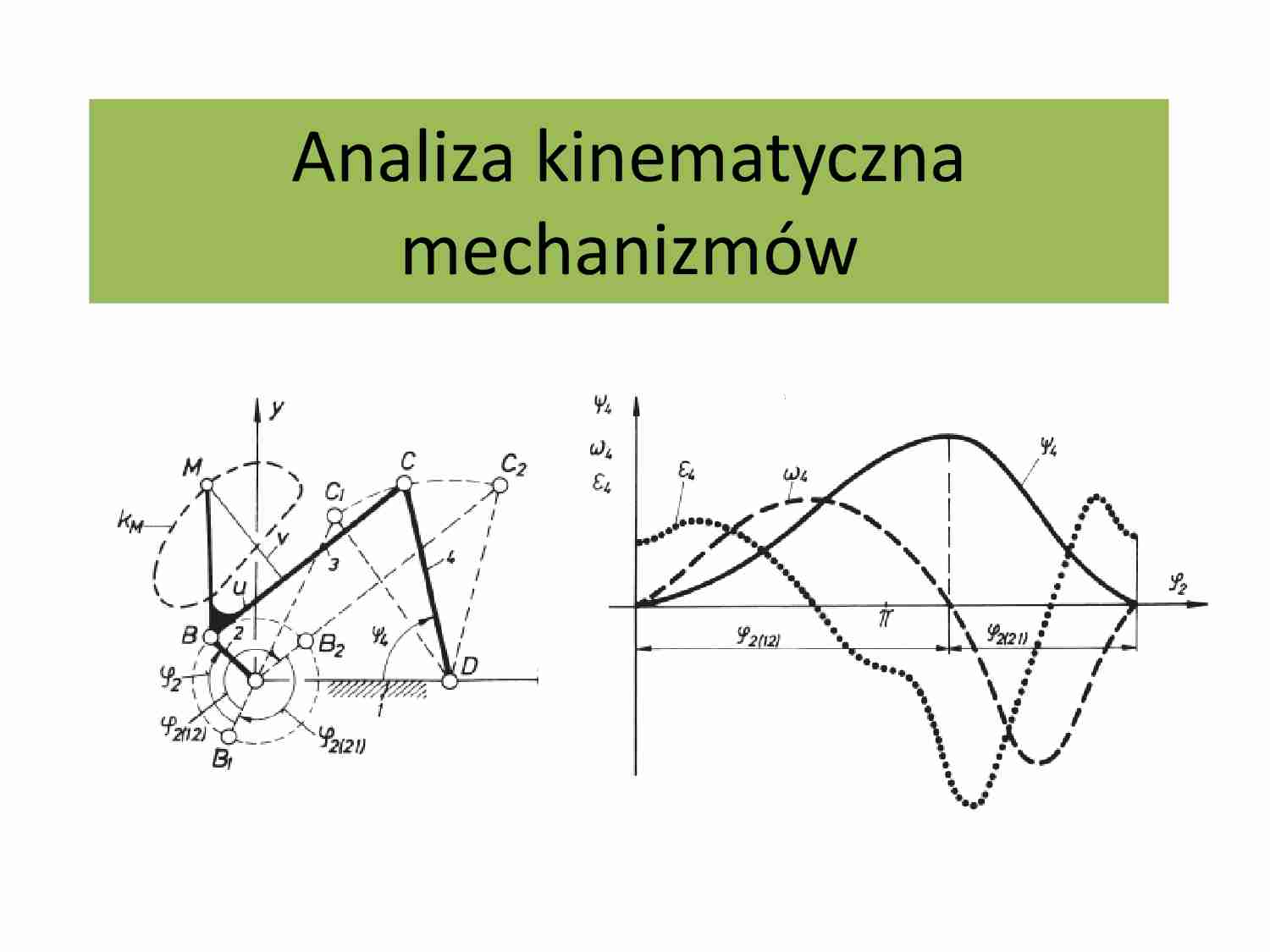


Analiza kinematyczna mechanizmów Kinematyka - dział mechaniki zajmujący się opisem ruchu ciał bez wnikania w przyczyny wywołujące zmiany ruchu. Kinematyka zajmuje się badaniem związków pomiędzy parametrami kinematycznymi (położenie, prędkośd, przyśpieszenie) członów czynnych a parametrami kinematycznymi pozostałych członów mechanizmu. Analiza kinematyczna mechanizmów - definicje Analiza kinematyczna mechanizmów - definicje A B r(t) r A = r(t) x y Dr(t) r’(t) vA = v(t) = Dr/Dt = dr/dt aA = a(t) = Dv/Dt = = dv/dt = d2r/dt2 a a1 a = a(t) w = w(t) = Da/Dt= da/dt = (t) = Dw/Dt= dw/dt = =d2a/dt2 Podstawowe parametry kinematyczne: Analiza kinematyczna mechanizmów - definicje Liniowe Kątowe Położenie r (t) a(t) Prędkość v =d r /dt w=da/dt Przyśpieszenie a =d v /dt a =d2 r /dt2 =dw/dt =d2a/dt2 Metody analizy kinematycznej: - analityczne, - wektorowe, - numeryczne. Analiza kinematyczna - wyznaczanie położeo członów, trajektorie punktów Trajektoria, tor punktu – miejsca geometryczne jego kolejnych położeo w przyjętym układzie odniesienia. Analiza kinematyczna - trajektorie punktów Analiza kinematyczna - trajektorie punktów Analiza kinematyczna - trajektorie punktów Analiza kinematyczna - trajektorie punktów Analiza kinematyczna - trajektorie punktów Analiza kinematyczna - trajektorie punktów B A C C’ B’ rBC Dj Analiza kinematyczna – wyznaczanie nowych położeo członów: metoda geometryczna B A C C’ B’ rBC j(t) Dane: j(t) Szukane: xc’, yc’ xB’ = AB cos j yB’ = AB sin j (xC’ – xB’)2 + (yC’ – yB’) 2 = BC2 yC’ = 0 Z układu równao otrzymamy: xC’ , yC’ y x Analiza kinematyczna – wyznaczanie nowych położeo członów: metoda analityczna Analiza kinematyczna – wyznaczanie nowych położeo członów B A D C C’ B’ Analiza kinematyczna – wyznaczanie nowych położeo członów: metoda geometryczna rBC Dj Analiza kinematyczna – wyznaczanie nowych położeo członów: metoda analityczna B A D C C’ B’ y x j(t) Dane: j(t) Szukane: xc’, yc’ xB’ = AB cos j yB’ = AB sin j (xC’ – xB’)2 + (yC’ – yB’) 2 = BC2 (xC’ – xD)2 + (yC’ – yD) 2 = CD2 rBC Z układu równao otrzymamy: xC’ , yC’ Analiza kinematyczna – wyznaczanie nowych położeo członów A D B B1 C E F Położenie - konfiguracja układu Analiza kinematyczna – wyznaczanie nowych
... zobacz całą notatkę






Komentarze użytkowników (0)