Sprawozdanie nr 1 Niezawodność systemów
Analiza danych niezawodnościowych
1) Cel ćwiczenia:
Zapoznanie się z podstawowymi możliwościami analizy danych niezawodnościowych
w programie Excel i pakiecie Weibull ++.
2) Wykonane zadania:
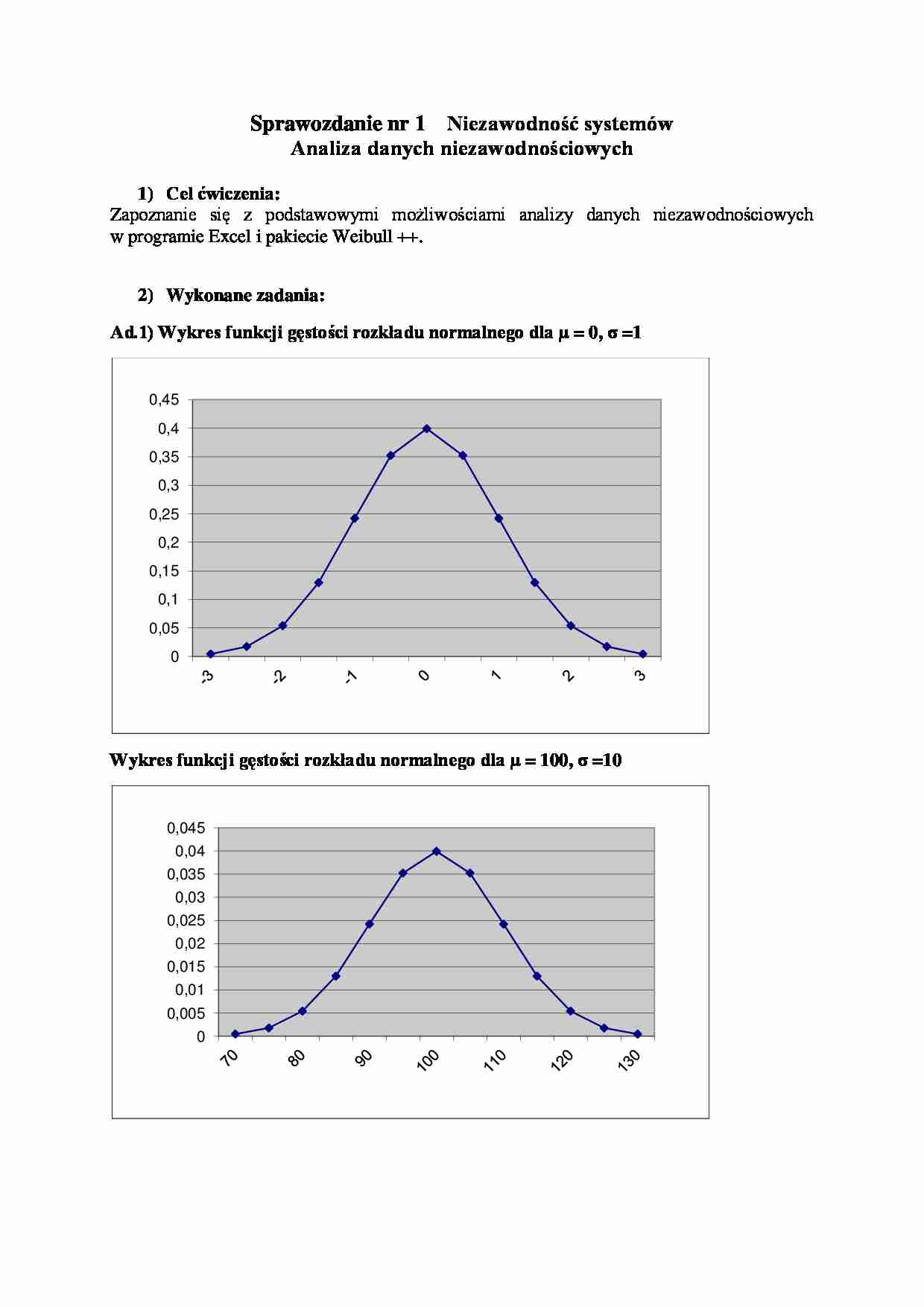
Ad.1) Wykres funkcji gęstości rozkładu normalnego dla μ = 0, σ =1
0,45
0,4
0,35
0,3
0,25
0,2
0,15
0,1
0,05
0
Wykres funkcji gęstości rozkładu normalnego dla μ = 100, σ =10
0,045
0,04
0,035
0,03
0,025
0,02
0,015
0,01
0,005
0
Ad.2) Wygenerowano:
a) n=20
b) n=1000
liczb będących realizacjami zmiennej losowej o rozkładzie normalnym z parametrami μ = 0,
σ =1 , a następnie dla wygenerowanych zestawów danych wyznaczono wartości minimalne
i maksymalne oraz narysowano histogramy.
a)
średnia
odchylenie
standard.
min
max
97,902
13,62317
129,1649
76,90866
b)
średnia
odchylenie
standard.
min
max
100,0999
9,831856
129,7499
70,1191
Zbiór danych (koszyk)
Więcej
116,1008757
103,0368028
89,97272996
76,90865712
Częstość
Histogram
8
7
6
5
4
3
2
1
0
Histogram
80
Częstość
70
60
50
40
30
20
10
0
Zbiór danych (koszyk)
Pierwszy histogram nie wskazuje na żaden typ rozkładu prawdopodobieństwa ze względu na
małą ilość danych, natomiast na podstawie histogramu drugiego można stwierdzić, że dane
reprezentują rozkład normalny. Dla zestawu b) estymatory są najbardziej zbliżone do wartości
rzeczywistych.
Ad.6)
Wykres probabilistyczny pakietu Weibull ++ dla rozkładu normalnego.
Wykres probabilistyczny pakietu Weibull ++ dla rozkładu wykładniczego.
Wykres probabilistyczny pakietu Weibull ++ dla rozkładu Weibulla.
Wykres probabilistyczny pakietu Weibull ++ dla rozkładu logistycznego.
Najlepsze dopasowanie danych uzyskano do rozkładu Weibulla, które można rozpoznać po
jak najmniejszych odchyleniach danych od rozkładu. Dopasowanie do rozkładu Weibulla
wskazuje na niewielkie różnice.
Ad.7) Przy pomocy Distribution Wizard potwierdzono ocenę dopasowania z powyższego
zadania.
Distribution Wizard wskazał najlepsze dopasowanie z rozkładem Weibull, następnie z
rozkładem wykładniczym, logistycznym i najmniejsze dopasowanie z rozkładem normalnym.
Ad.8) Dokonano estymacji parametrów dla każdego rozkładu metodą MLE (największej
wiarygodności).
Parametry otrzymane po estymacji to:
Dla rozkładu logistycznego: μ =8109,0011, σ =4337,7660
Dla rozkładu Weibulla: Beta=1,1165, Eta=8726,6695
Dla rozkładu wykładniczego: λ =0,0001
Dla rozkładu normalnego: μ =8109,0011, σ =7383,0746
... zobacz całą notatkę





Komentarze użytkowników (0)