To tylko jedna z 8 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


0. Początki fizyki współczesnej 0.1 Promieniowanie ciała doskonale czarnego Ciało doskonale czarne - pochłania całkowicie padające na nie promieniowanie elektromagnetyczne, niezależnie od temperatury tego ciała, kąta padania i widma padającego promieniowania. Współczynnik pochłaniania dla takiego ciała jest równy jedności dla dowolnej długości fali. Ciało doskonale czarne nie istnieje w rzeczywistości, ale dobrym jego modelem jest duża wnęka z niewielkim otworem, pokryta od wewnątrz czarną substancją (np. sadzą). Powierzchnia otworu zachowuje się niemal jak ciało doskonale czarne - promieniowanie wpadające do wnęki odbija się wielokrotnie od jej ścian i jest niemal całkowicie pochłaniane, natomiast parametry promieniowania wychodzącego z jej wnętrza zależą tylko od temperatury wewnątrz wnęki. W rzeczywistości wszystkie obiekty niebieskie emitują promieniowanie termiczne (pod warunkiem, że ich temperatura jest powyżej zera bezwzględnego lub -273,15 stopni Celsjusza), ale żaden z obiektów nie emituje promieniowania idealnie; obiekty emitują/pochłaniają niektóre długości fali świetlnej bardziej niż inne. Takie nierówna efektywność utrudnia studiowanie wzajemnego oddziaływania światła, ciepła i materii przy użyciu normalnych obiektów.
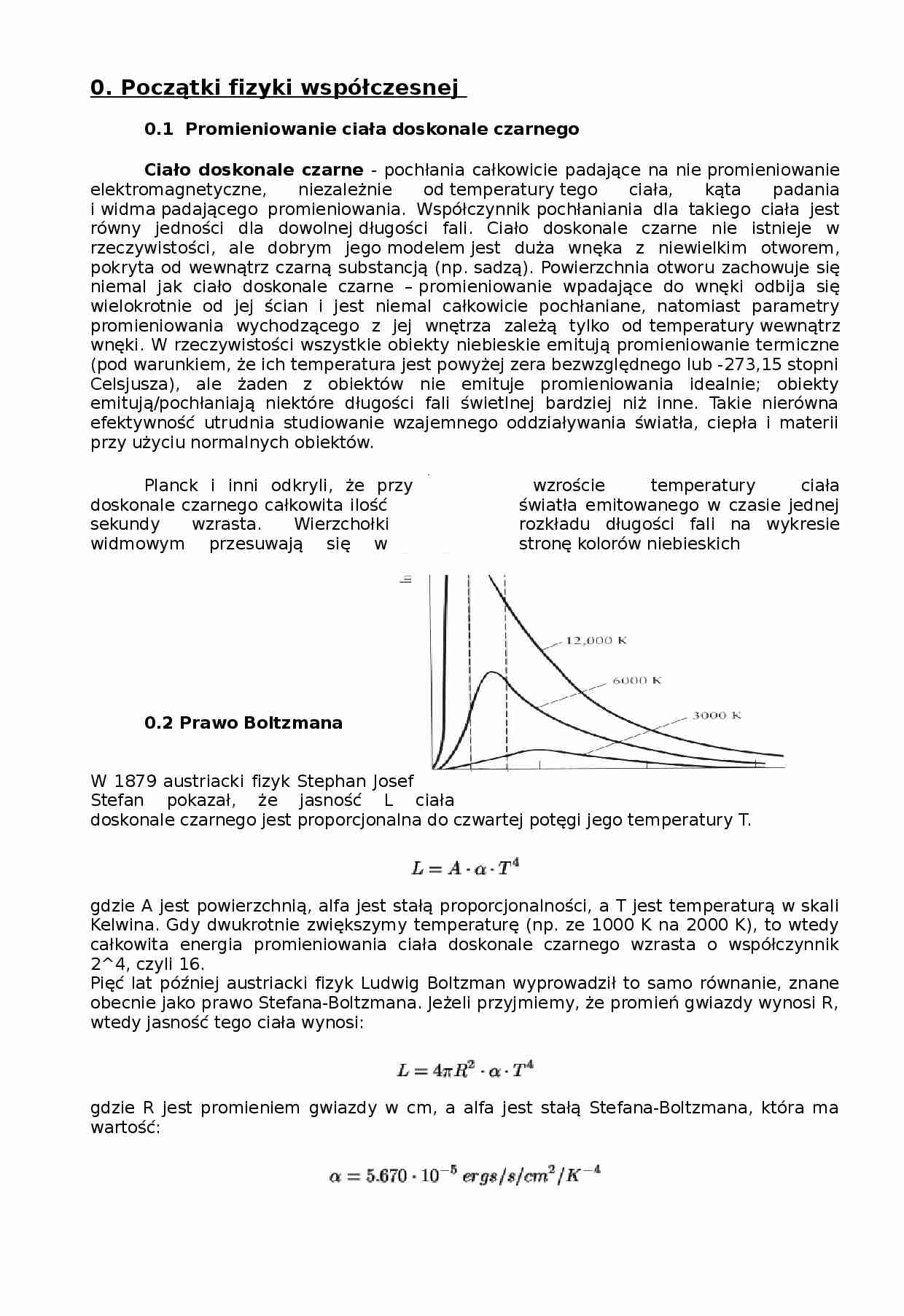
Planck i inni odkryli, że przy wzroście temperatury ciała doskonale czarnego całkowita ilość światła emitowanego w czasie jednej sekundy wzrasta. Wierzchołki rozkładu długości fali na wykresie widmowym przesuwają się w stronę kolorów niebieskich 0.2 Prawo Boltzmana
W 1879 austriacki fizyk Stephan Josef Stefan pokazał, że jasność L ciała doskonale czarnego jest proporcjonalna do czwartej potęgi jego temperatury T.
gdzie A jest powierzchnią, alfa jest stałą proporcjonalności, a T jest temperaturą w skali Kelwina. Gdy dwukrotnie zwiększymy temperaturę (np. ze 1000 K na 2000 K), to wtedy całkowita energia promieniowania ciała doskonale czarnego wzrasta o współczynnik 2^4, czyli 16.
Pięć lat później austriacki fizyk Ludwig Boltzman wyprowadził to samo równanie, znane obecnie jako prawo Stefana-Boltzmana. Jeżeli przyjmiemy, że promień gwiazdy wynosi R, wtedy jasność tego ciała wynosi:
gdzie R jest promieniem gwiazdy w cm, a alfa jest stałą Stefana-Boltzmana, która ma wartość:
0.3 Prawo przesunięć Wien'a:
Opisuje promieniowanie elektromagnetyczne emitowane przez ciało doskonale czarne. Ze wzrostem temperatury widmo
(…)
… destruktywnej wygaszone.
3.3 Warunki ciągłości funkcji falowych i ich pochodnych:
3.4 Zjawisko tunelowania, przykłady:
Zjawisko tunelowe zwane też efektem tunelowym - zjawisko przejścia cząstki przez barierę potencjału o wysokości większej niż energia cząstki, opisane przez mechanikę kwantową. Z punktu widzenia fizyki klasycznej stanowi paradoks łamiący klasycznie rozumianą zasadę zachowania energii…
…).
Dla innych przypadków wstawiamy do równania inny V i obliczamy… No dobrze: o ile mniej więcej wiemy o co chodzi z tymi możliwymi energiami, to co może oznaczać funkcja falowa ψ? W każdym podręczniku od mechaniki kwantowej przeczytamy, że sens fizyczny ma dopiero kwadrat modułu funkcji falowej |ψ(r)|2, który jest wszędzie nieujemny i jest gęstością prawdopodobieństwa znalezienia cząstki w punkcie r[3…
…, czyli płytki ze szkła, na której gęsto zarysowane są rysy pełniące rolę przesłon pomiędzy szczelinami. Obraz interferencyjny widoczny w tym przypadku na ekranie jest znacznie wyraźniejszy i jaśniejszy niż przy użyciu jedynie dwóch szczelin.
2. Równanie Schrödingera / funkcja falowa:
Funkcja falowa to w mechanice kwantowej funkcja zmiennych konfiguracyjnych np. położenia, o wartościach zespolonych, będąca…
…], dla bariery potencjału o szerokości d znacznie mniejszej niż droga zaniku funkcji falowej, prawdopodobieństwo przetunelowania elektronu zależy wykładniczo od szerokości tej bariery.
3.5 Pułapki elektronowe - nanokrystality:
Proszki, których ziarna są małe - w zakresie nanometrycznym - mają inny kolor niż proszki o większym ziarnie. Każdy nanokrystalit stanowi studnię potencjału dla elektronu zamkniętego…
… charakterystyki układu, wykluczają się nawzajem. Przykładowo, dokładny pomiar pędu wyklucza dokładną znajomość położenia, a do pełnego opisu tego, co dzieje się z cząstką, potrzebna jest znajomość jej pędu i położenia. Zasada komplementarności ma ścisły związek z zasadą nieoznaczoności omówioną w rozdziale o Wernerze Heisenbergu. Bohr wziął również udział wraz z Heisenbergiem i Bornem w formułowaniu…
... zobacz całą notatkę






Komentarze użytkowników (0)