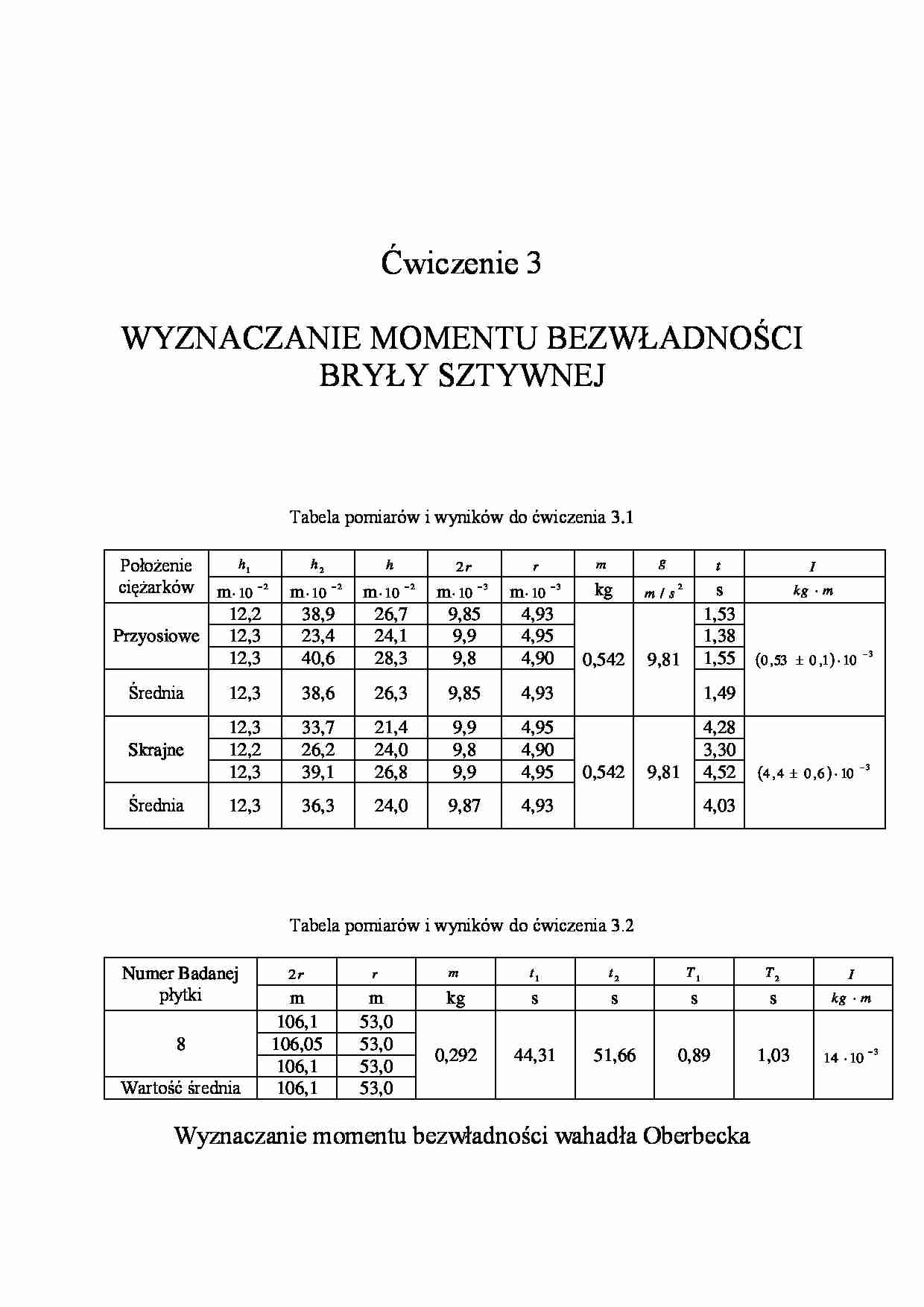
Ćwiczenie 3 WYZNACZANIE MOMENTU BEZWŁADNOŚCI BRYŁY SZTYWNEJ Tabela pomiarów i wyników do ćwiczenia 3.1 Położenie ciężarków 1 h 2 h h r 2 r m g t I m 2 10 m 2 10 m 2 10 m 3 10 m 3 10 kg 2 / s m s m kg Przyosiowe 12,2 38,9 26,7 9,85 4,93 0,542 9,81 1,53 3 10 1 , 0 53 , 0 12,3 23,4 24,1 9,9 4,95 1,38 12,3 40,6 28,3 9,8 4,90 1,55 Średnia 12,3 38,6 26,3 9,85 4,93 1,49 Skrajne 12,3 33,7 21,4 9,9 4,95 0,542 9,81 4,28 3 10 6 , 0 4 , 4 12,2 26,2 24,0 9,8 4,90 3,30 12,3 39,1 26,8 9,9 4,95 4,52 Średnia 12,3 36,3 24,0 9,87 4,93 4,03 Tabela pomiarów i wyników do ćwiczenia 3.2 Numer Badanej płytki r 2 r m 1 t 2 t 1 T 2 T I m m kg s s s s m kg 8 106,1 53,0 0,292 44,31 51,66 0,89 1,03 3 10 14 106,05 53,0 106,1 53,0 Wartość średnia 106,1 53,0 Wyznaczanie momentu bezwładności wahadła Oberbecka 1. Obliczenia Położenie ciężarków Przyosiowe: 2 3 4 4 2 4 2 2 6 2 2 2 2 3 2 2 10 53 , 0 10 32 , 5 6 , 52 10 2 , 21 2 , 13 6 , 52 10 8 , 52 22 , 2 81 , 9 10 3 , 24 542 , 0 10 3 , 26 2 10 4 , 26 2 22 , 2 81 , 9 10 3 , 24 542 , 0 10 3 , 26 2 10 4 , 26 2 49 , 1 81 , 9 ) 10 93 , 4 ( 542 , 0 2 2 m kg I h h gt mr I Położenie ciężarków Skrajne: 2 3 4 4 4 2 2 2 2 3 2 2 10 4 , 4 10 7 , 43 0 , 48 10 8 , 158 2 , 13 0 , 48 482 , 0 24 , 16 81 , 9 10 3 , 24 542 , 0 10 0 , 24 2 10 1 , 24 2 03 , 4 81 , 9 ) 10
(…)
…
100 % 0 , 011 %
Ponieważ błąd I jest o kilka rzędów wielkości mniejszy od wartości I, wynosząc jedynie jej
0,011% możemy go uznać za pomijalny.
…
... zobacz całą notatkę





Komentarze użytkowników (0)