To tylko jedna z 5 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


#
ĆWICZENIE NR 84
WYZNACZANIE DŁUGOŚCI FALI ŚWIETLNEJ ZA POMOCĄ SIATKI DYFRAKCYJNEJ
I. Zestaw przyrządów:
1. Siatki dyfrakcyjne
2. Filtry interferencyjne
3. Monochromator z zasilaczem
4. Oświetlacz z zasilaczem
5. Ekran ze skalą i szczeliną
6. Ława optyczna z podziałką
II. Cel ćwiczenia
1. Wyznaczenie stałej siatki dyfrakcyjnej
2. Wyznaczenie chromatycznej zdolności rozdzielczej oraz dyspersji kątowej siatki dyfrakcyjnej
3. Wyznaczenie długości fal światła przepuszczanego przez filtry interferencyjne
III. Przebieg pomiarów i opracowanie wyników
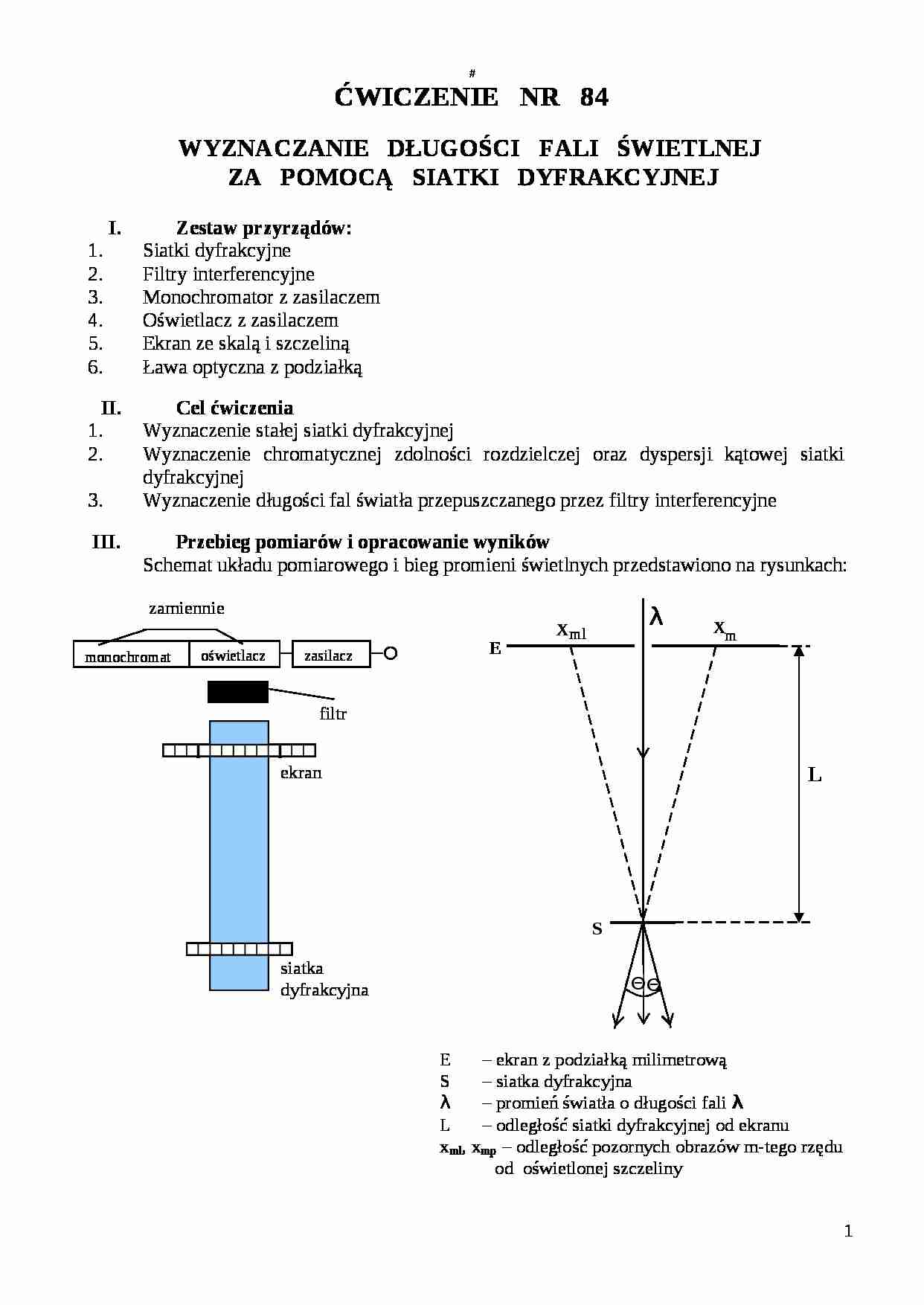
Schemat układu pomiarowego i bieg promieni świetlnych przedstawiono na rysunkach:
zamiennie
xml λ m
E
filtr
ekran L
S
siatka
dyfrakcyjna ΘΘ
E - ekran z podziałką milimetrową
S - siatka dyfrakcyjna
λ - promień światła o długości fali λ
L - odległość siatki dyfrakcyjnej od ekranu
xml, xmp - odległość pozornych obrazów m-tego rzędu od oświetlonej szczeliny
1
Zadania podstawowe
1. Wyznaczanie stałej siatki dyfrakcyjnej
a) na ławie optycznej w odległości L od ekranu ustawić siatkę dyfrakcyjną, a za ekranem ustawić źródło światła monochromatycznego: monochromator lub oświetlacz z filtrem interferencyjnym,
b) wiązkę światła monochromatycznego skierować na szczelinę w ekranie,
c) patrząc przez siatkę dyfrakcyjną zaobserwować świecącą szczelinę w ekranie i jej pozorne obrazy na tle ekranu ze skalą,
d) przy pomocy ruchomych wskazówek przymocowanych do ekranu zaznaczyć położenia
pozornych obrazów szczeliny tworzonych przez promienie ugięte m - tego rzędu i odczytać
ich odległości xml i xmp od szczeliny
e) obliczyć średnią wartość xm odległości pozornego obrazu od oświetlonej szczeliny
x ml + x mp
x m = 2
oraz niepewność Δxm np. metodą różniczki zupełnej
f) wyznaczyć sinusy kątów ugięcia dla pierwszego i drugiego rzędu dyfrakcji korzystając ze
xm
wzoru:
(…)
… i drugiego rzędu
dyfrakcji odpowiednio m = 1 lub m = 2
d = mλ (sinΘm )śr
oraz niepewność Δd np. metodą pochodnej logarytmicznej, a następnie wyznaczyć wartość średnią dśr oraz niepewność Δdśr .
i) niepewność Δ(sin Θm) wyznaczyć np. metodą różniczki zupełnej dla każdego Θm,
a następnie porównać te wartości z niepewnością pomiaru Δ(sin Θm)śr wynikającą
z rozrzutu wyników otrzymanych dla różnych wartości L…
... zobacz całą notatkę






Komentarze użytkowników (0)