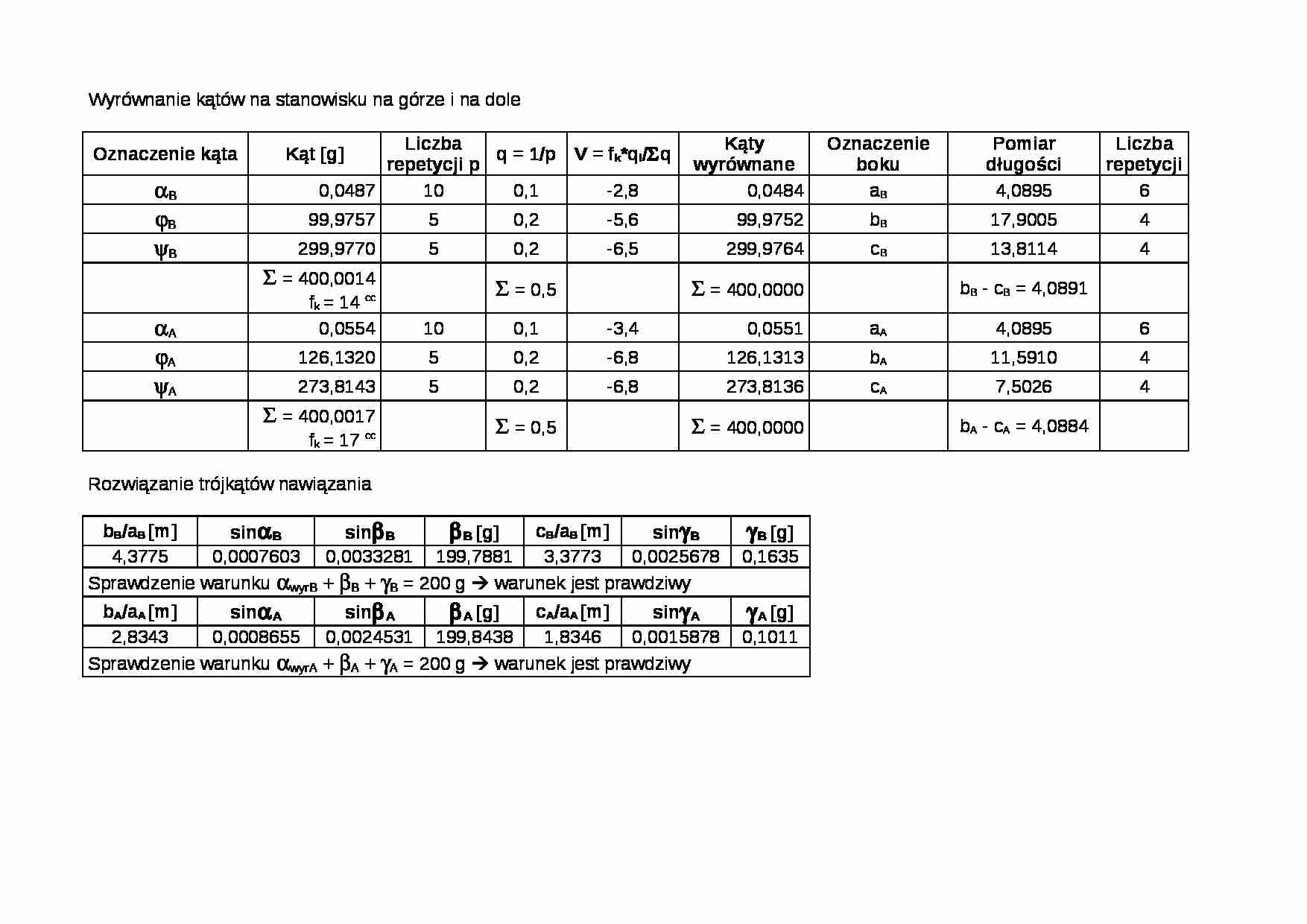
Wyrównanie kątów na stanowisku na górze i na dole
Oznaczenie kąta
Kąt [g]
Liczba repetycji p
q = 1/p
V = fk*qi/Σq
Kąty wyrównane
Oznaczenie boku
Pomiar długości
Liczba repetycji
αB 0,0487
10
0,1
-2,8
0,0484
aB 4,0895
6
ϕB 99,9757
5
0,2
-5,6
99,9752
bB 17,9005
4
ψB 299,9770
5
0,2
-6,5
299,9764
cB 13,8114
4
Σ = 400,0014
fk = 14 cc Σ = 0,5
Σ = 400,0000
bB - cB = 4,0891
αA 0,0554
10
0,1
-3,4
0,0551
aA 4,0895
6
ϕA 126,1320
5
0,2
-6,8
126,1313
bA 11,5910
4
ψA 273,8143
5
0,2
-6,8
273,8136
cA 7,5026
4
Σ = 400,0017
fk = 17 cc Σ = 0,5
Σ = 400,0000
bA - cA = 4,0884
Rozwiązanie trójkątów nawiązania
bB/aB [m]
sinαB
sinβB
βB [g]
cB/aB [m]
sinγB
γB [g]
4,3775
0,0007603
0,0033281
199,7881
3,3773
0,0025678
0,1635
Sprawdzenie warunku αwyrB + βB + γB = 200 g warunek jest prawdziwy
bA/aA [m]
sinαA
sinβA
βA [g]
cA/aA [m]
sinγA
γA [g]
2,8343
0,0008655
0,0024531
199,8438
1,8346
0,0015878
0,1011
Sprawdzenie warunku αwyrA + βA + γA = 200 g warunek jest prawdziwy
Obliczanie azymutu AA-208:
drogą I : „197” - B - P2 - A - „208”
AB-197 = 108,1347 [ g ]
AB-P2 = AB-197
... zobacz całą notatkę





Komentarze użytkowników (0)