Wykład - pole elektryczne w dielektrykach

Nasza ocena:

3
Pobrań: 7
Wyświetleń: 637
Komentarze: 0
Notatek.pl

Pobierz ten dokument za darmo

Pobierz notatkę
Podgląd dokumentu
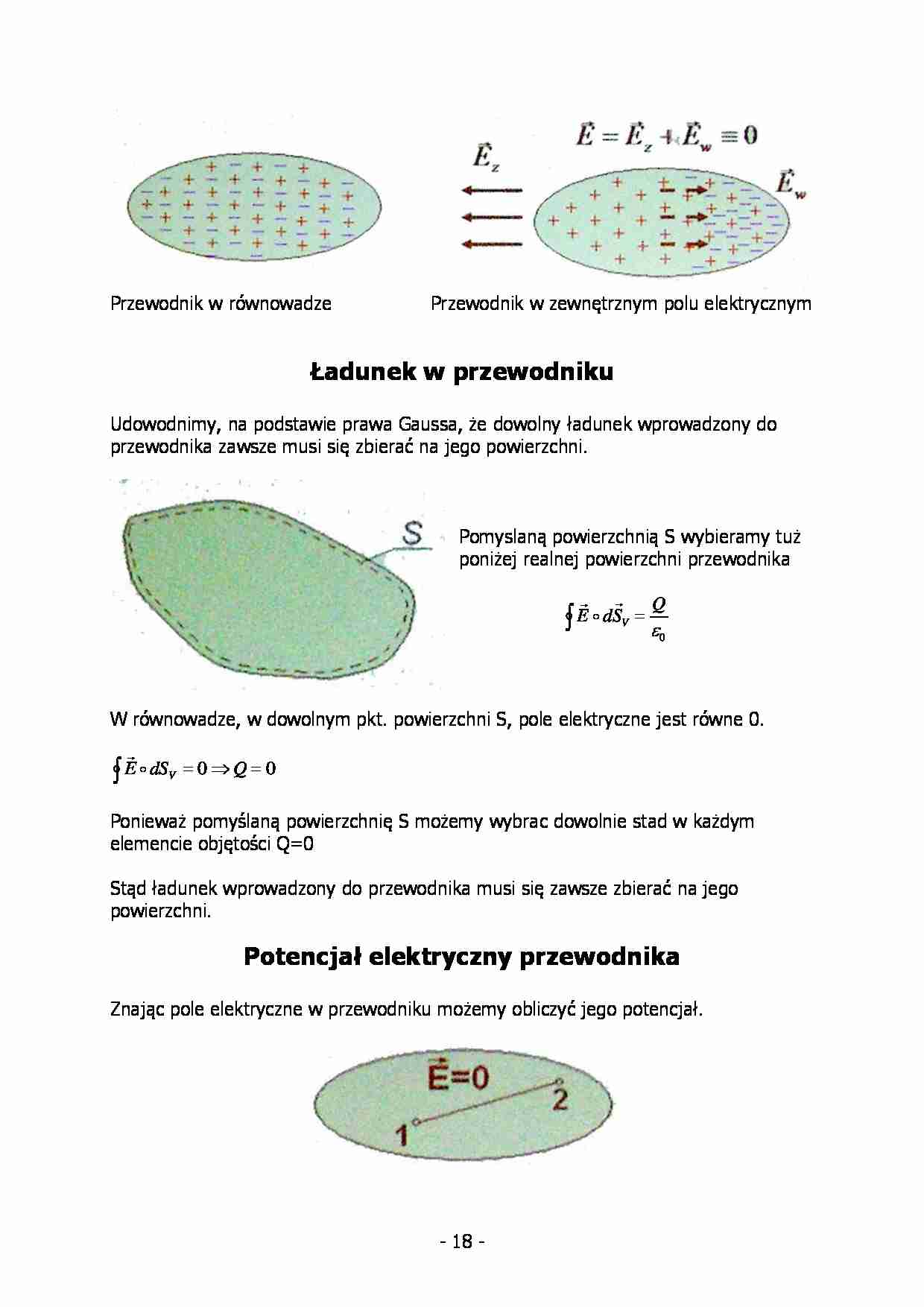
Wykład - pole elektryczne w dielektrykach - strona 1 Wykład - pole elektryczne w dielektrykach - strona 2 Wykład - pole elektryczne w dielektrykach - strona 3

Fragment notatki:

Przewodnik w równowadze
Przewodnik w zewnętrznym polu elektrycznym
Ładunek w przewodniku
Udowodnimy, na podstawie prawa Gaussa, że dowolny ładunek wprowadzony do
przewodnika zawsze musi się zbierać na jego powierzchni.
Pomyslaną powierzchnią S wybieramy tuż
poniżej realnej powierzchni przewodnika
 
Q
E  dSV 

0
W równowadze, w dowolnym pkt. powierzchni S, pole elektryczne jest równe 0.

 E  dS
V
0Q 0
Ponieważ pomyślaną powierzchnię S możemy wybrac dowolnie stad w każdym
elemencie objętości Q=0
Stąd ładunek wprowadzony do przewodnika musi się zawsze zbierać na jego
powierzchni.
Potencjał elektryczny przewodnika
Znając pole elektryczne w przewodniku możemy obliczyć jego potencjał.
- 18 -
 
V  V2  V1    E  dr  0  V2  V1  const
2
1
Przewodnik stanowi obszar stałego potencjału. Pole elektryczne jest zawsze
prostopadłe do powierzchni stałego potencjału, czyli jest zawsze prostopadła do
powierzchni przewodnika.
  
E  n
0
- 19 -
Pole elektryczne w dielektrykach
W dielektryku, nie zawierającym swobodnych ładunków elektrycznych, obserwujemy
ruch ładunków związanych polem dodatnim jonowym na odległości mikroskopowej.
W objętości dielektryka tworzą się dipole elektryczne o momencie dipolowym p
Zewnętrzne pole elektryczne indukuje moment dipolowy p związany z rozdzieleniem
na odległości L ładunku q cząstki.
Jeżeli w dielektryku mamy N cząsteczek na jednostkę objętości to wypadkowy
moment dipolowy na jednostkę objętości jest równy:



P  N  p  N qL
Wektor ten nazywany jest wektorem polaryzacji.
Ponieważ cząsteczki pozostają obojętne elektrycznie średni ładunek w objętości
dielektryka pozostaje równy 0.
Dodatkowy ładunek Qz pojawi się na powierzchni zewnętrznej dielektryka. Ładunek
ten wytworzy dodatkowe pole elektryczne skierowane przeciwnie do pola
zewnętrznego.
- 20 -
Dla powierzchni S dielektryka wartość tego ładunku wynosi:
Qz  S  L  N  q
z 

Qz
 N qL  P
S
Ten dodatkowy ładunek powierzchniowy wytwarza w objętości dielektryka pole
wewnętrzne Ew skierowane przeciwnie do pola zewnętrznego E

P



1 
Ew  Z 
 Ew  P
0
0
0
Stad wypadkowe pole w dielektryku:

 1 
Ed  E  P
0
Zakłada się, ze moment dipolowy jednostki objętości indukowany polem E jest do
tego pola proporcjonalny


P   0    Ed
Stała  nosi nazwę podatności elektrycznej dielektryka. Podstawiając:









E
E
E
E
 Ed 

Ed  E    Ed  Ed 

1  
1  
Przenikalność dielektryczna
od pola zewnętrznego.
 1 mówi nam ile razy pole w dielektryku jest mniejsze
Prawo Gaussa w dielektrykach
Obliczymy pole elektrostatyczne wytworzone prze z dwie płyty naładowane
ładunkami   i  
Bez dielektryka
Z dielektrykiem
- 21 -

Q  S
E  dS v 


0
0

Q ' (   z )  S (  P )  S

 E  dS v  
0
0
0
 
( 0  E  P)  dS v    S  Q

Wprowadzamy wielkość wektorową – wektor indukcji elektrycznej:


 
C 

D  dS v  Q
D  0  E  P   2 

m

(…)

…
wewnętrzne Ew skierowane przeciwnie do pola zewnętrznego E

P



1 
Ew  Z 
 Ew  P
0
0
0
Stad wypadkowe pole w dielektryku:

 1 
Ed  E  P
0
Zakłada się, ze moment dipolowy jednostki objętości indukowany polem E jest do
tego pola proporcjonalny


P   0    Ed
Stała  nosi nazwę podatności elektrycznej dielektryka. Podstawiając:









E
E
E
E
 Ed 

Ed  E    Ed  Ed…
... zobacz całą notatkę



Komentarze użytkowników (0)

Zaloguj się, aby dodać komentarz