To tylko jedna z 73 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


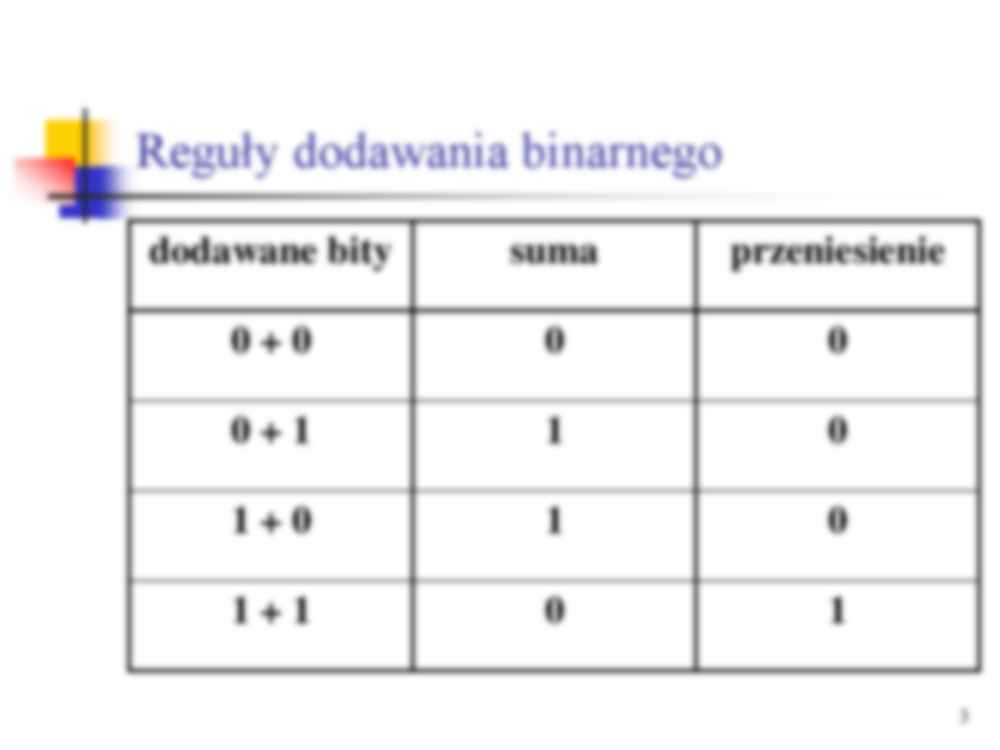
Wstęp do programowania Wykład 4, 5, 6 1 2 Arytmetyka binarna 3 Reguły dodawania binarnego dodawane bity suma przeniesienie 0 + 0 0 0 0 + 1 1 0 1 + 0 1 0 1 + 1 0 1 4 Dodawanie 1 0 0 0 1 1 1 1 0 0 0 1 0 0 0 1 1 0 1 0 0 0 0 0 0 0 0 0 1 1 1 0 1 0 0 1 1 1 1 1 1 0 1 0 1 1 0 1 5 Odejmowanie 1 1 1 0 0 1 0 0 1 1 0 1 1 0 1 1 0 0 1 0 1 1 1 0 1 0 0 1 0 1 0 0 1 0 0 1 6 Mnożenie 1 1 1 1 * 1 0 1 ---------------- 1 1 1 1 + 0 0 0 0 1 1 1 1 ----------------- 1 0 0 1 0 1 1 7 Dzielenie 1 1 0 ---------------- 1 0 0 1 0 : 11 1 1 ---------- 1 1 1 1 -------------- 0 8 Ułamki w zapisie binarnym 9 Liczba zapisana w systemie dwójkowym w postaci: ( c k … c0 , c-1 c-2 … c-n )2 jest równa liczbie w systemie dziesiątkowym: (c k *2 k +… +c 0 *2 0 + c -1 *2 -1 +… + c -n *2 -n ) 10 10 Kropka pozycyjna pełni tę samą rolę co przecinek w notacji dziesiątkowej 11.101 = 1*21 +1*20 + 1*2-1 +0*2-2 + 1*2-3 = część całkowita część ułamkowa = 2 + 1 + 1/2 + 0 + 1/8 = 8 5 3 8 1 8 4 3 10.011 + 110.11 = 1001.001 11 1 0 0 1 1 + 1 1 0 1 1 1 0 0 1 0 0 1 12 0101 . 0 4 1 16 1 16 4 16 1 16 5 11 . 10 2 1 4 1 2 4 3 2 13 Zamiana ułamka dziesiętnego na ułamek dwójkowy 0.125 2 * 0.125 = 0.25 0.25 2 * 0.25 = 0.5 0.5 2 * 0.5 = 1.0 0.0 koniec 0.125 10 = 0.0012 spr. 0.001 2 = 1/8 = 0.125 14 Nie każdą liczbę zapisaną w postaci ułamka dziesiętnego da się dokładnie przedstawić w postaci ułamka dwójkowego. 15 0.3 2 * 0.3 = 0.6 0.6 2 * 0.6 = 1.2 0.2 2 * 0.2 = 0.4 0.4 2 * 0.4 = 0.8 0.8 2 * 0.8 = 1.6 0.6 …. otrzymany ułamek dwójkowy jest okresowy 0.01001 2 = 0.25 + 0.03125 = 0.2812510 duży błąd zaokrąglenia 16 Reprezentacja liczb całkowitych 17 W systemie binarnym nie ma możliwości zapisu liczb ujemnych. Konieczna jest jego modyfikacja. 18 System kodowania znaku i modułu (ZM) Skrajny lewy bit - bit znaku 0 – liczba dodatnia 1 – liczba ujemna np. przy użyciu 8 bitów zapis liczb 20 10 i -510 20 10 = –5 10 = 0 0 0 1 0 1 0 0 1 0 0 0 0 1 0 1 19 Reprezentacja zera Zero może być reprezentowane na dwa
(…)
… binarną o 1
są nieskomplikowane, dodawanie w kodzie U1 jest dosyć prosto
realizowalne sprzętowo.
31
Kod uzupełnień do 2
System U2
32
System uzupełnień do dwóch
n
n
n
n
tylko jedna liczba służy do oznaczania zera
operacje binarnego dodawania i odejmowania
mogą być wykonywane w ten sam sposób
znak nie jest oddzielony od wartości liczby
każda liczba, której najbardziej znaczący bit
jest jedynką musi być liczbą ujemną
33
System uzupełnień do dwóch
Najbardziej znaczący bit jest wykorzystywany
zarówno jako bit znaku, jak i bit wpływający na
wartość liczby.
Najbardziej znaczący bit liczby n-bitowej ma
przypisany rząd -2n-1
waga
-2n-1
2n-2
2n-3
….
22
21
20
cyfra
bn-1
bn-2
bn-3
……
b2
b1
b0
34
-27 26 25 24 23 22 21 20
-128 64
32
1
0 1 0 0 1 1
0
16
8
4
2
1
-128+16+2+1= -109
35
Kodowanie liczby ujemnej…
… otrzymać kod dwójkowy,
w którym zachowany byłby naturalny porządek
rosnący kolejnych słów kodowych.
Na przykład dla 3 bitowego kodu słowa kodowe
kolejnych liczb układałyby się następująco: 000,
001, 010, 011, 100, 101, 110, 111.
Słowo kodowe 000 powinno określać liczbę
najmniejszą, a słowo kodowe 111 liczbę
największą.
45
Zapis dwójkowy z nadmiarem
n
n
Wartość binarna słowa kodowego jest
równa kodowanej…
… – wykładnik (cecha)
58
Zapis liczb w komputerze
Zastępujemy podstawę potęgi 10
podstawą 2
59
Aby ujednolicić wyniki obliczeń
numerycznych wykonywanych na różnych
platformach sprzętowych, wprowadzono
ściśle określony standard zapisu
zmiennoprzecinkowego IEEE 754.
60
Standard IEEE 754
definiuje dwa rodzaje liczb zmiennoprzecinkowych:
n 32-bitowe (pojedynczej precyzji - ang. single precision)
n 64-bitowe…
... zobacz całą notatkę






Komentarze użytkowników (0)