To tylko jedna z 6 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


Laboratorium Materiałów Konstrukcyjnych i Eksploatacyjnych – P.Wr. W–9
Termiczna rozszerzalność materiałów konstrukcyjnych
Cel ćwiczenia
Wyznaczenie współczynników liniowej rozszerzalności cieplnej α różnych materiałów.
Wprowadzenie
Każda substancja zmienia swoje wymiary pod wpływem temperatury. Zasadą jest,
że ciała rozszerzają się przy wzroście temperatury, ponieważ jest to tożsame ze
wzrostem średniej odległości między jego atomami. Oczywiście są wyjątki. Najbardziej znanym spośród nich jest lód, którego objętość właściwa rośnie podczas spadku
temperatury. Innymi przykładami są bizmut, gal, krzem i german. Wywołane termicznie zmiany wymiarów można wyrazić dwoma współczynnikami: liniowym α i
objętościowym β współczynnikiem rozszerzalności cieplnej. Ten ostatni jest stosowany
głownie do płynów, podczas gdy pierwszy do ciał stałych. Liniowy współczynnik
rozszerzalności cieplnej jest zdefiniowany następującymi wzorami
α=
1 ∆L ε
1 dL
=
=
,
∆T L0 ∆T L0 dT
(1)
gdzie: ∆T – przyrost temperatury; L0 – długość w temperaturze T0; ∆L – przyrost długości odpowiadający wzrostowi temperatury o ∆T; ε = ∆L/L0 – wydłużenie względne.
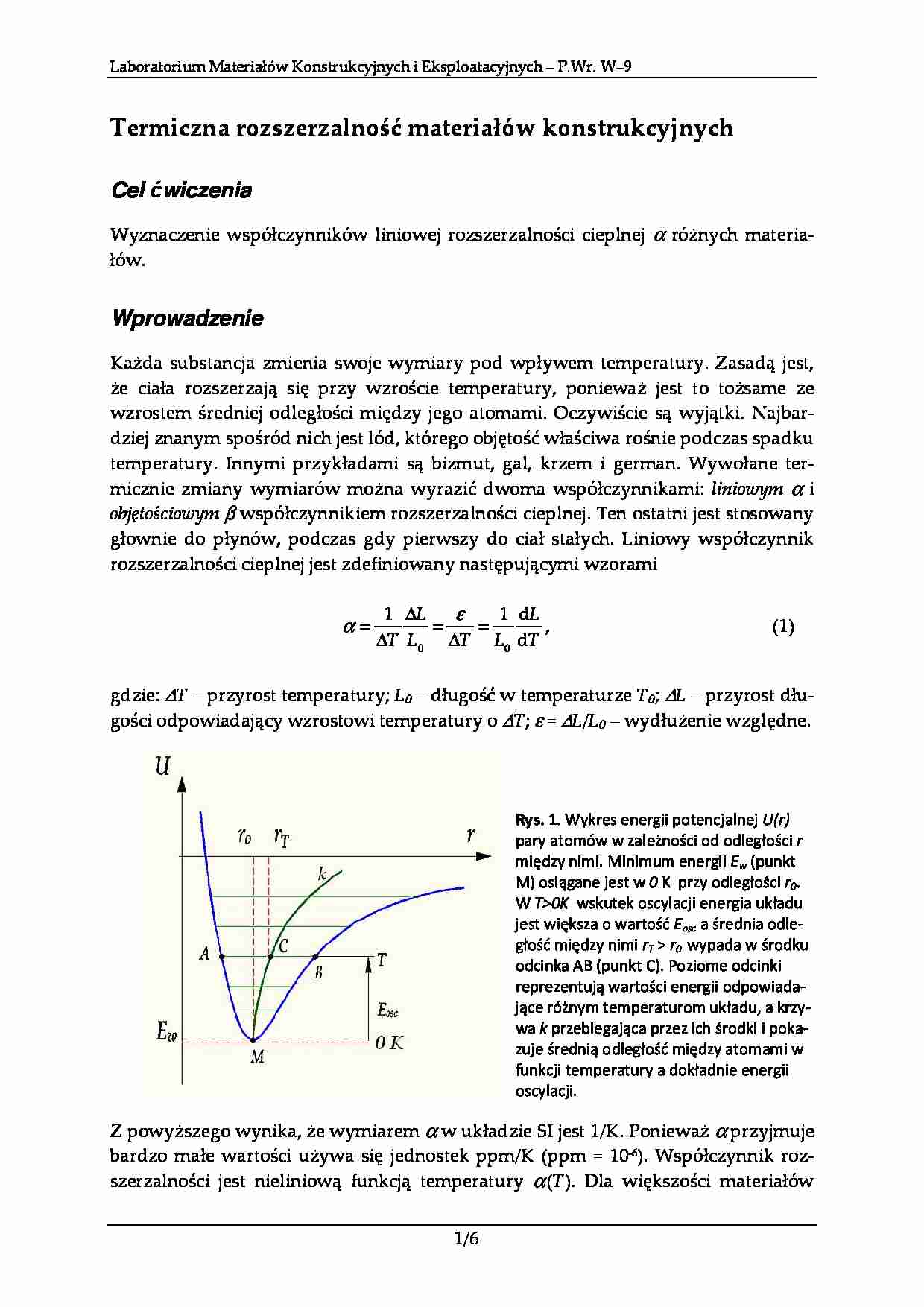
Rys. 1. Wykres energii potencjalnej U(r)
pary atomów w zależności od odległości r
między nimi. Minimum energii Ew (punkt
M) osiągane jest w 0 K przy odległości r0.
W T0K wskutek oscylacji energia układu
jest większa o wartość Eosc a średnia odległość między nimi rT r0 wypada w środku
odcinka AB (punkt C). Poziome odcinki
reprezentują wartości energii odpowiadające różnym temperaturom układu, a krzywa k przebiegająca przez ich środki i pokazuje średnią odległość między atomami w
funkcji temperatury a dokładnie energii
oscylacji.
Z powyższego wynika, że wymiarem α w układzie SI jest 1/K. Ponieważ α przyjmuje
bardzo małe wartości używa się jednostek ppm/K (ppm = 10-6). Współczynnik rozszerzalności jest nieliniową funkcją temperatury α (T). Dla większości materiałów
1/6
Laboratorium Materiałów Konstrukcyjnych i Eksploatacyjnych – P.Wr. W–9
zależność ta jest słaba, dlatego w niezbyt dużym zakresie temperatur wartość α
można uznać za stałą. Jak widać wydłużenie próbki można wyliczyć z
∆L = α∆TL0
(2)
Wydłużenie cieplne α ciał (Rys.1.) wynika z niesymetrycznego przebiegu wykresu energii potencjalnej U atomów w funkcji odległości między nimi r. Jego ogólna
postać to U(r) = a/r m – b/r n, gdzie a, b, n, m 0 oraz m n pewne stałe. Człon pierwszy reprezentuje energię związaną z
siłami odpychającymi a drugi z przyciągającymi. Minimum tej energii
(punkt M) przypadający w odległości
r0 między atomami zwany jest energią
wiązania Ew. Jest to położenie równowagi osiągane w temperaturze zera
bezwzględnego 0 K. W temperaturze T
0 K atomy oscylują, co podnosi energię układu o wartość energii oscylacji
Eosc, która jest proporcjonalna do T.
Punkty A i B odpowiadają energii
układu w skrajnym wychyleniu atomów. W temperaturze T średnia odległość między atomami rT (punkt C)
wyznaczona środkiem odcinka AB jest
większa od r0. Jest to
... zobacz całą notatkę






Komentarze użytkowników (0)