Średni bezwzględny błąd prognozy MAE (Mean Absolute Error) określany także jako
średnia modułów błędów prognoz, oblicza się według wzoru:
Gdzie nt błąd bezwzględny prognozy na czas t obliczony na podstawie prognoz
wygasłych.
Prognoza wygasła – jest to prognoza sporządzona na moment taki, dla którego znana
(dostępna) jest już wartość prognozowanej zmiennej.
Prognozy wygasłe używane do oszacowania błędu prognozy autentycznej muszą być
sporządzone według takiej procedury i na taką odległość, jak prognoza autentyczna.
Średni błąd kwadratowy prognozy MSE (Mean Squared Error)
Średni bezwzględny błąd procentowy MAPE (Mean Absolute Percentage Error)
Ex post – szacowanie błędu prognozy na podstawie prognoz wygasłych
Przykład:
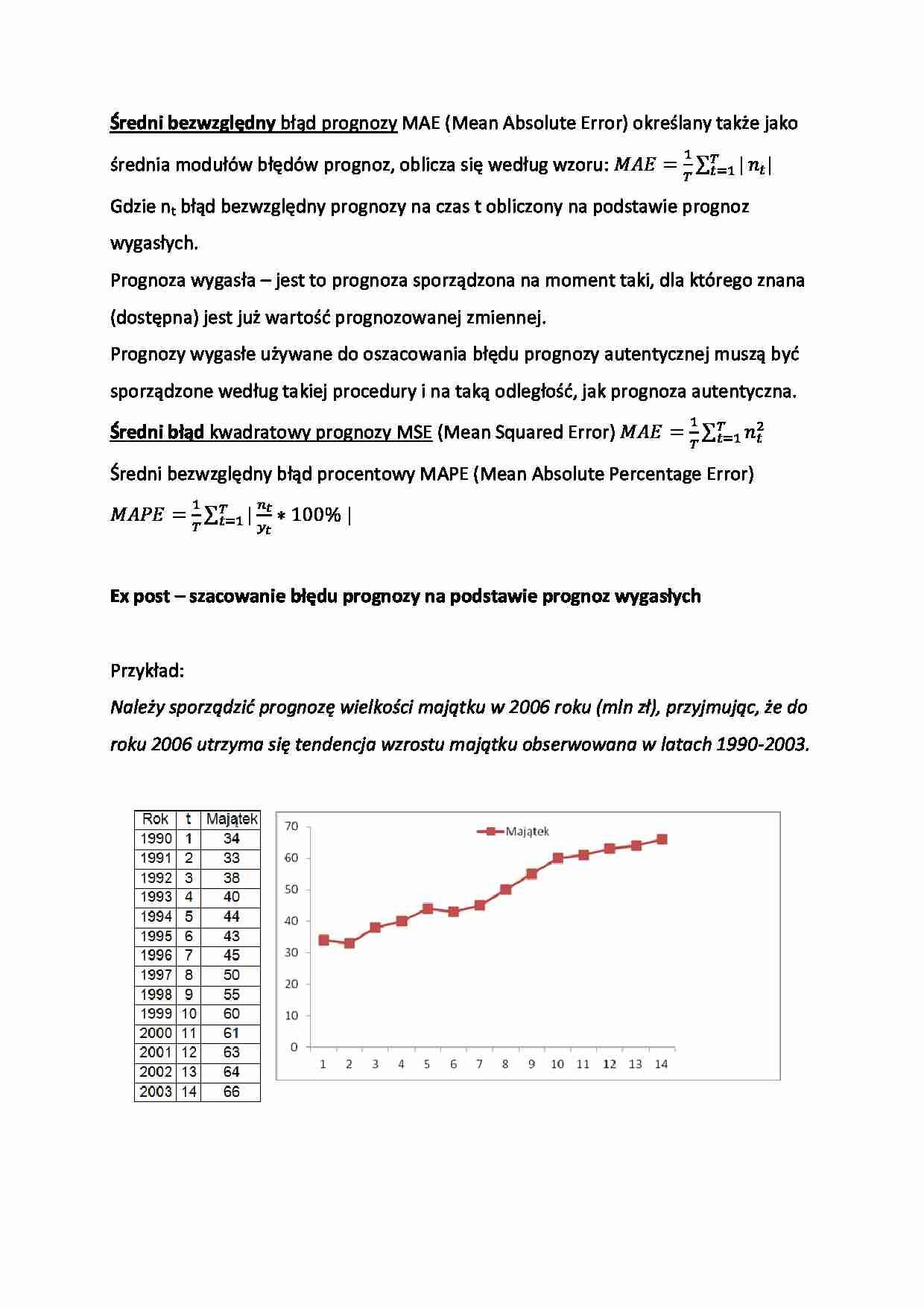
Należy sporządzić prognozę wielkości majątku w 2006 roku (mln zł), przyjmując, że do
roku 2006 utrzyma się tendencja wzrostu majątku obserwowana w latach 1990-2003.
Prognoza:
W latach 1990-2003 majątek wzrastał według trendu liniowego: Y=at+b, t=1 dla 1990,
Δt=1
Po zastosowaniu mnk (metody najmniejszych kwadratów), równanie trendu majątku
ma postać: Y=2,75t + 29,11
Prognoza, obliczana jako ekstrapolacja trendu na rok 2006 ma postać: y*2006=
2,75*17+29,11= 77,2 mln zł
Szacowanie błędu prognozy ex-post
Materiał statystyczny do obliczenia prognoz wygasłych
Przyjęto minimalną liczebność zbioru na poziomie 5 oraz wzięto pod uwagę odcinki
początkowe danych, czyli zbiory rozpoczynające się od t=1, czyli:
Rok
1990
1991
1992
1993
1994
Zbiór 1-5
t
1
2
3
4
5
yt
34
33
38
40
44
Rok
1990
1991
1992
1993
1994
1995
Zbiór 1-6
t
1
2
3
4
5
6
yt
34
33
38
40
44
43
Rok
1990
1991
1992
1993
1994
1995
1996
Zbiór 1-7
t
1
2
3
4
5
6
7
yt
34
33
38
40
44
43
45
Itd. aż do zbioru 1-11
Procedura obliczania prognoz wygasłych:
Przyjęta procedura polega na ekstrapolacji na trzy lata naprzód (wyznaczona
prognoza dotyczyła 2006 roku, dane kończą się na 2003 roku, stąd zachowując
zasadę. Prognozy wygasłe używane do oszacowania błędu prognozy autentycznej
muszą być sporządzane według takiej procedury i na taką odległość jak prognoza
autentyczna. Otrzymuje się 3-letni okres prognozowania trendu liniowego,
wyznaczonego klasyczną metodą mnk.
Przykładowe obliczenia dla trzech pierwszych zbiorów są następujące:
Kompletne wyliczenia dla zbiorów od 1-5 do 1-11 zawiera tabela:
Zbiór
Współczynnik
Wyraz
Moment
Wartość
Prognoz
Błąd
Moduł
kierunkowy
wolny
prognozowania t
empiryczna
a dla t
prognozy
błędu
dla t
prognozy
{1,5}
2,70
29,70
8
50
51,30
1,30
1,30
{1,6}
2,29
30,67
9
55
51,24
-3,76
3,76
{1,7}
2,11
31,14
10
60
52,21
-7,79
7,79
{1,8}
2,27
30,64
11
61
55,65
-5,35
5,35
{1,9}
2,53
29,78
12
63
60,18
-2,82
2,82
{1,10}
2,80
28,80
13
64
65,20
1,20
1,20
{1,11}
2,86
28,55
14
66
68,64
2,64
2,64
Prognoza i jej dokładność:
Średnia modułów błędów prognoz wygasłych wynosi 3,55. Gdyby zatem w
przeszłości, systematycznie z roku na rok, dokonywano aktualizacji modelu i
prognozowano majątek na 3 lata
... zobacz całą notatkę





Komentarze użytkowników (0)