Stochastyczne szacowanie błędu prognozy Ex Ante

Nasza ocena:

3
Pobrań: 119
Wyświetleń: 553
Komentarze: 0
Notatek.pl

Pobierz ten dokument za darmo

Pobierz notatkę
Podgląd dokumentu
Stochastyczne szacowanie błędu prognozy Ex Ante - strona 1 Stochastyczne szacowanie błędu prognozy Ex Ante - strona 2 Stochastyczne szacowanie błędu prognozy Ex Ante - strona 3

Fragment notatki:

Ex Ante- stochastyczne szacowanie błędu prognozy
Model może być rozumiany jak funkcja, która opisuje powiązanie między zmienną
objaśnianą a zmiennymi objaśniającymi, może być konstruowany na gruncie założeń
stochastycznych (probabilistycznych). Główne założenia takiego podejścia są
następujące:
 Istnieje pewien model hipotetyczny (nasze przypuszczenie), czyli zależność
zmiennej objaśnianej od zmiennych objaśniających opisywana jako:
Gdzie: - parametry
X- zmienne objaśniające
 Prawdziwa zależność zmiennej Y od zmiennych X jest zakłócana przez wiele
różnych czynników, z których niektóre mają charakter stochastyczny (losowy),
określane literą E (składnik losowy), czyli:
Przykład:
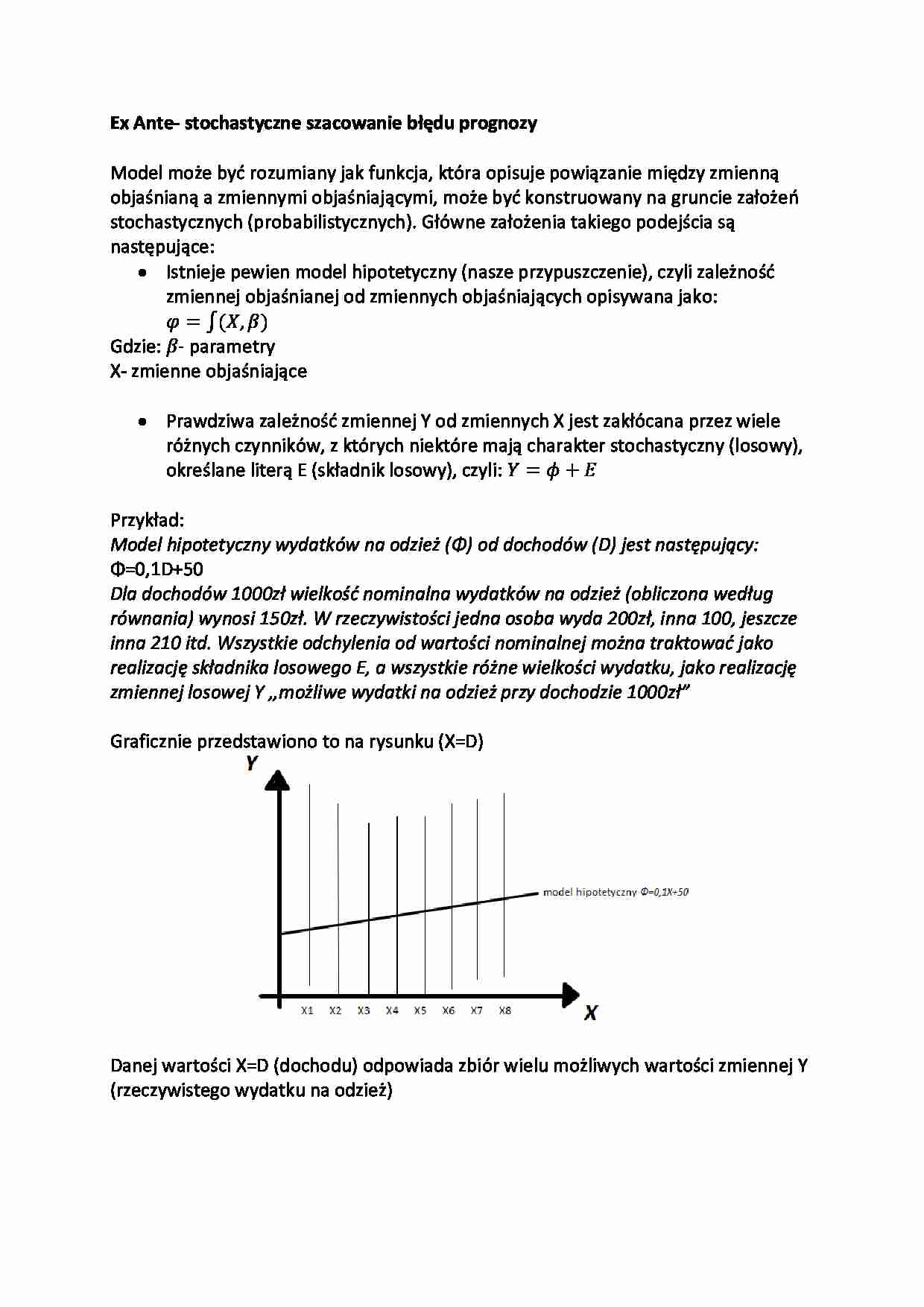
Model hipotetyczny wydatków na odzież (Φ) od dochodów (D) jest następujący:
Φ=0,1D+50
Dla dochodów 1000zł wielkość nominalna wydatków na odzież (obliczona według
równania) wynosi 150zł. W rzeczywistości jedna osoba wyda 200zł, inna 100, jeszcze
inna 210 itd. Wszystkie odchylenia od wartości nominalnej można traktować jako
realizację składnika losowego E, a wszystkie różne wielkości wydatku, jako realizację
zmiennej losowej Y ,,możliwe wydatki na odzież przy dochodzie 1000zł”
Graficznie przedstawiono to na rysunku (X=D)
Danej wartości X=D (dochodu) odpowiada zbiór wielu możliwych wartości zmiennej Y
(rzeczywistego wydatku na odzież)
Stosowana terminologia jest następująca:
Proces stochastyczny- zbiór możliwych wyników obserwacji zmiennej objaśnianej (Y)
Funkcja regresji- model hipotetyczny(Φ)
Wyróżnia się następujący podział:
Z uwagi na losowość zmiennych objaśniających- regresja z
-nielosowymi zmiennymi objaśniającymi
-losowymi zmiennymi objaśniającymi
Z uwagi na złożenie składnika losowego i modelu hipotetycznego:
-regresja ze składnikiem losowym addytywnym, czyli: Y=Φ+E
-regresja ze składnikiem losowym multiplikatywnym, czyli Y= Φ*E
Z uwagi na postać analityczną modelu hipotetycznego
-regresja liniowa czyli Φ=ΣbkXk
-nieliniowa, na przykład wykładnicza
Z uwagi na typ powiązania zmiennej objaśnianej ze zmiennymi objaśniającymiregresja:
 Klasyczna
 Segmentowa
 Lokalna
Z uwagi na wariancje i korelacje składników losowych- regresja:
 Ze sferycznymi składnikami losowymi (składniki losowe mają identyczne
wariancje i są wzajemnie nieskorelowane)
 Z niesferycznymi składnikami losowymi (składniki losowe mają różne
wariancje lub są skorelowane)
Z uwagi na probabilistyczny rozkład składników losowych, regresja:
 Normalna (gdy proces stochastyczny składników losowych ma nieosobliwy
rozkład normalny)
 Nie-normalna (gdy proces stochastyczny składników losowych ma rozkład inny
niż normalny)
Najczęściej rozpatruje się układy z następującymi założeniami:
 Zmienne objaśniające są nielosowe
 Regresja ze składnikiem losowym addytywnym, czyli Y= Φ+E
Regresja liniowa, czyli Φ= ΣbkXk
 Regresja klasyczna
 Ze sferycznymi składnikami losowymi (składniki losowe mają identyczne
wariancje-zwykle równe 0 i są wzajemnie nieskorelowane)
 Regresja normalna (gdy proces stochastyczny ... zobacz całą notatkę



Komentarze użytkowników (0)

Zaloguj się, aby dodać komentarz