To tylko jedna z 8 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
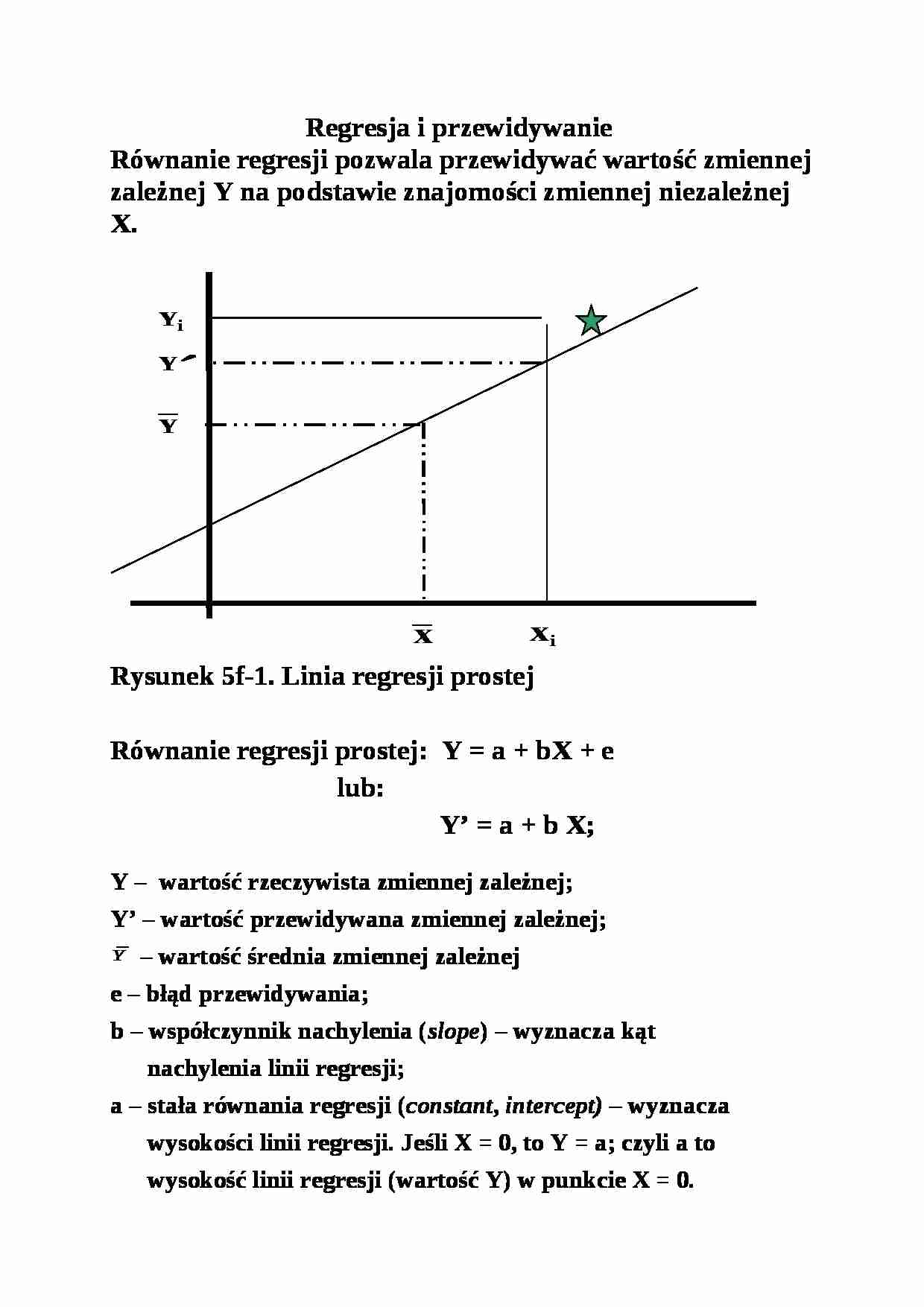


Regresja i przewidywanie Równanie regresji pozwala przewidywać wartość zmiennej zależnej Y na podstawie znajomości zmiennej niezależnej X. Rysunek 5f-1. Linia regresji prostej
Równanie regresji prostej: Y = a + bX + e
lub:
Y' = a + b X; Y - wartość rzeczywista zmiennej zależnej; Y' - wartość przewidywana zmiennej zależnej; - wartość średnia zmiennej zależnej e - błąd przewidywania; b - współczynnik nachylenia (slope) - wyznacza kąt nachylenia linii regresji; a - stała równania regresji (constant, intercept) - wyznacza wysokości linii regresji. Jeśli X = 0, to Y = a; czyli a to wysokość linii regresji (wartość Y) w punkcie X = 0.
Analizowane dane (zmienna zależną niezależną) możemy przedstawić w postaci standaryzowanej (jako odchylenia poszczególnych wyników od średniej całkowitej):
Dane w postaci standaryzowanej mają, z założenia, średnią: = 0 i wariancję: σ2 = 1. Dla danych standaryzowanych równanie regresji ma postać: Y' = β X
(opuszczamy w równaniu a, gdyż wynosi ono zero). Równanie regresji w postaci standaryzowanej jest bardzo wygodne gdyż eliminuje wpływ jednostek pomiaru na wartość zmiennych. Wszystkie zmienne wyrażone są w tych samych jednostkach: jednostkach odchylenia standardowego.
Analiza regresji umożliwia (analogicznie jak w wypadku ANOVA) rozłożenie sumy kwadratów (SS) zmiennej zależnej Y (Σy2) na dwie składowe: SS przewidywaną na podstawie równania regresji - SS nie przewidywalną przez równanie regresji - SS błędu (SSerror) lub SS resztową (residual -- ).
(porównaj rysunek na poprzedniej stronie) Ponieważ dwa wyrażenia po prawej stronie równania (w nawiasach) są nieskorelowane ze sobą, zachodzi równość:
Σy2 = SSreg + SSres
r2 = Jak widać z ostatniego wzoru, r2 informuje o tym, jaką proporcję całkowitej sumy kwadratów zmiennej zależnej można przewidzieć na podstawie zmiennej niezależnej (i równania regresji). Z wzoru tego widać też, że im większe jest SSreg (tzn. im bliżej linii regresji położone są punkty na wykresie, por. strony 4 i 5) tym wyższa jest korelacja (r i r2).
Istotność współczynnika regresji dana jest wzorem:
F = = k= liczba zmiennych niezależnych, N = wielkość próby (dla jednej zm. niezależnej: df
(…)
… niezależna na zmienną zależną. Wielkości współczynników b są nieporównywalne, bo zależą od skali pomiarowej (zmiana jednostki pomiaru powoduje zmianę współczynnika b). Y' = β1 X1, + β2 X2, + ... + βn Xn
Analiza regresji pozwala Wybrać zbiór predyktorów (zmiennych niezależnych), spośród wszystkich predykatorów poddanych analizie, który zapewnia najlepsze przewidywanie zmiennej Y; przy doborze predyktorów brane jest pod uwagę ich wzajemne skorelowanie. Ocenić wagi poszczególnych predyktorów. Oszacować jaki procent całkowitej sumy kwadratów zmiennej zależnej można przewidzieć na podstawie wszystkich zmiennych niezależnych uwzględnionych w równaniu regresji. Miarą tego efektu jest współczynnik determinacji (r2 lub R2). Dla odróżnienia od korelacji prostej (r) współczynnik korelacji wielokrotnej oznacza…
… i r2).
Istotność współczynnika regresji dana jest wzorem:
F = = k= liczba zmiennych niezależnych, N = wielkość próby (dla jednej zm. niezależnej: df1 = 1, df2 = N - 2). Jeśli istotne jest r to istotne jest też r2 (przy identycznym alfa).
Istnieją metody analizy regresji krzywoliniowej, analizujące rozrzut punktów względem jakieś krzywej.
KORELACJA I REGRESJA WIELOKROTNA
(multiple correlation and…
... zobacz całą notatkę






Komentarze użytkowników (0)