To tylko jedna z 29 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
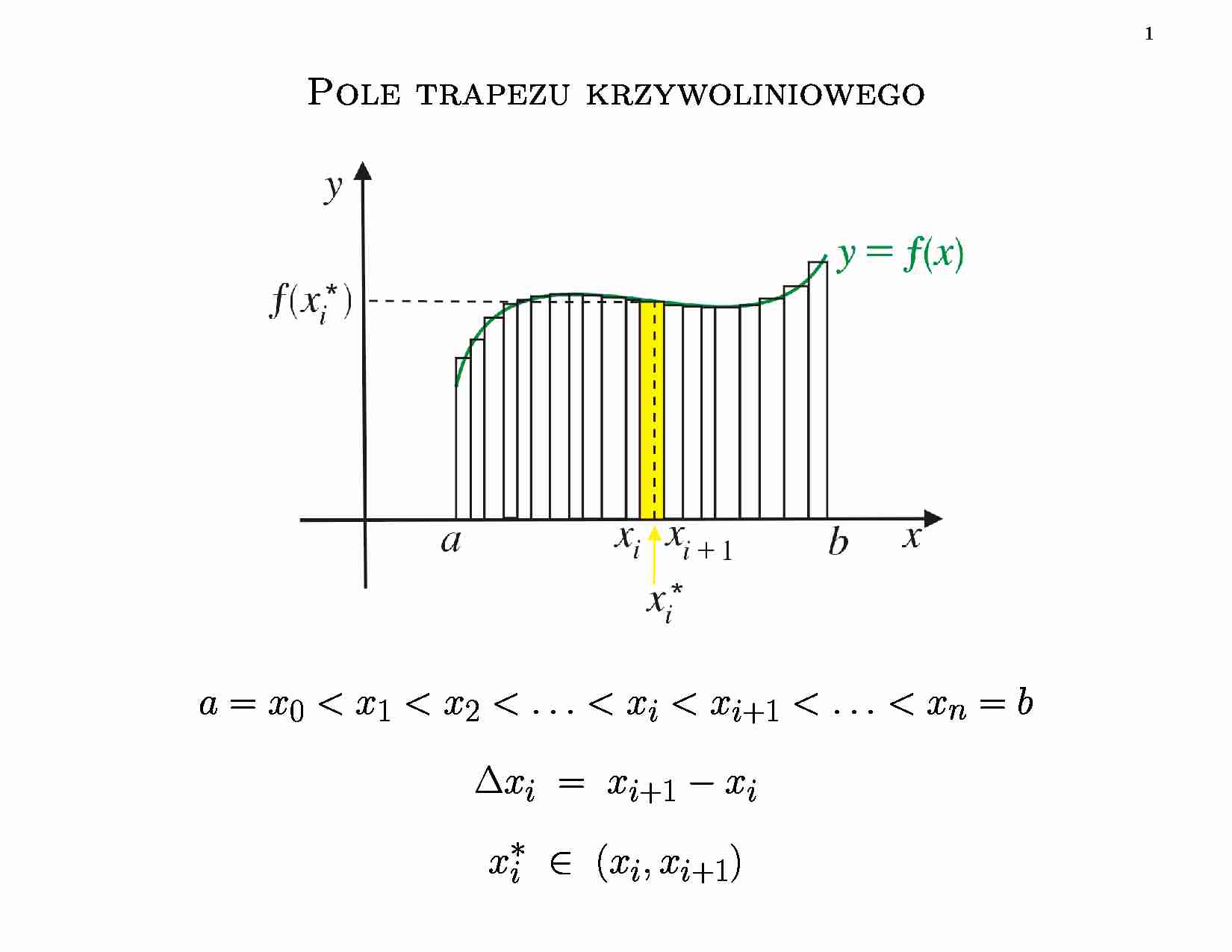


1 Pole trapezu krzywoliniowego a = x 0
(…)
….
16
Całka oznaczona a całka nieoznaczona
Niech f będzie funkcją ciągłą na [a, b] . Wówczas dla dowolnego
x ∈ [a, b] funkcja f jest całkowalna na [a, x] .
Oznaczmy:
Φ(x) =
x
a
f (t) dt.
Wówczas:
• Φ jest funkcją zmiennej x ∈ [a, b]
• Φ jest funkcją ciągłą
• Φ jest funkcją różniczkowalną i
d x
f (t) dt = f (x).
Φ (x) =
dx a
17
• Zatem Φ jest funkcją pierwotną dla funkcji f taką, że
Φ(a) =
Φ(b) =
a
a
b
a
f (t) dt = 0
f (t) dt.
Niech
f (x) dx = F (x) + C.
Wówczas istnieje stała C0 taka, że
Φ(x) = F (x) + C0
dla dowolnego x ∈ [a, b] .
18
(Leibnitza - Newtona)
Twierdzenie
Jeżeli funkcja f jest ciągła na [a, b] a F jest funkcją pierwotną
dla funkcji f , to
b
a
f (x) dx = F (b) − F (a).
Wzór powyższy nosi nazwę podstawowego wzoru rachunku całkowego
i wyraża związek pomiędzy całką oznaczoną…
… oznaczonej
• Jeżeli f jest funkcją ciągłą i nieujemną na przedziale [a, b] , to
b
a
f (x) dx = |P |.
5
• Jeżeli f jest funkcją ciągłą i ujemną na przedziale [a, b] , to
b
a
f (x) dx = − |P |.
6
Przykład
Oblicz z definicji całkę oznaczoną:
b
a
Przykład
dx.
(Funkcji niecałkowalnej w sensie Riemanna)
Wykaż, że funkcja Dirichleta
D(x) =
1
x∈Q
0
x∈R
Q
nie jest funkcją…
… całkę oznaczoną:
3
x 9 − x2 dx
b)
1
Twierdzenie
0
−1
x2 e
−x3
dx
c)
2
π
1
π
1
sin x
2 dx
x
(Całkowanie przez części)
Załóżmy, że funkcje
f
i
g
są różniczkowalne a
f , g są funkcjami ciągłymi w przedziale [a, b] . Wówczas
b
a
f (x) · g (x) dx = f (x) · g(x)
b
a
−
b
a
f (x) · g(x) dx.
21
Przykład
Oblicz całkę oznaczoną:
a)
π
2
0
x sin 2x dx
b)
e
1
e
x | ln x| dx
22
Całki niewłaściwie
Całki niewłaściwie…
… pierwszego rodzaju (na przedziale nieograniczonym)
Definicja
Założmy, że funkcja
f
jest funkcją określoną na
przedziale [a, +∞) i całkowalną na dowolnym przedziale [a, A] .
Całkę niewłaściwą pierwszego rodzaju na
[a, +∞)
definiujemy
wzorem:
+∞
a
f (x) dx =
lim
A
A→+∞ a
f (x) dx.
Jeżeli granica ta istnieje i jest właściwa (skończona), to mówimy, że
całka niewłaściwa jest zbieżna. Jeżeli granica nie istnieje…
... zobacz całą notatkę






Komentarze użytkowników (0)