To tylko jedna z 29 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


Polaryzacja światła
W najbardziej ogólnym przypadku pole elektryczne i magnetyczne
fali elektromagnetycznej ma postać wektorową
E r , t ) E r , t exp j r , t
E r , t)
- wektor amplitudy, r , t faza, r -wektor położenia,
t-czas.
Dla płaskiej fali monochromatycznej rozchodzącej się w
kierunku z możemy napisać:
E z, t ) E0 exp j kz t
gdzie E0 można przedstawić jako:
mx exp j x
E0
my exp j y
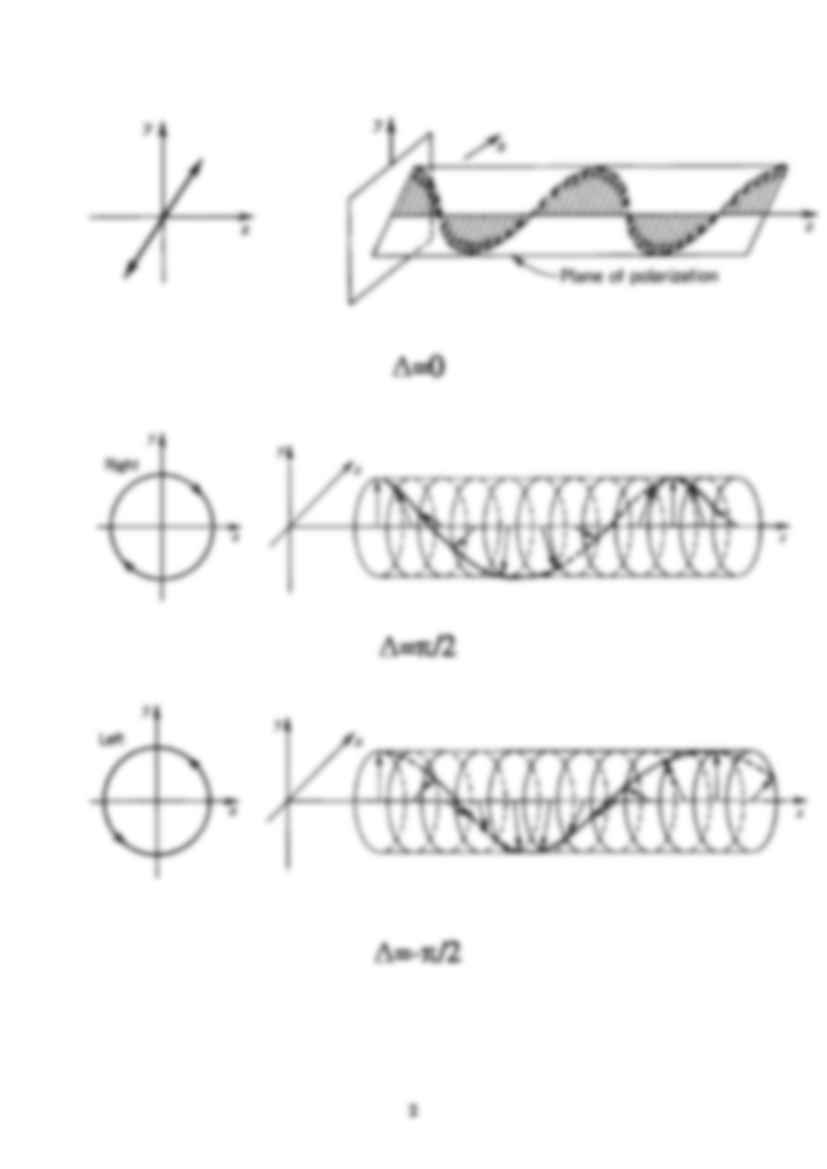
w zależności od różnicy faz =y-x obserwujemy różne
stany polaryzacji
1
=0
=/2
=-/2
2
Geometryczny opis stanu polaryzacji
Parametry opisujące elipsę stanu polaryzacji to azymut kąt
eliptyczności i skrętność stanu polaryzacji
-4545
znak ujemny dla lewoskretnych polaryzacji
Czasami używa się także parametru nazywanego
eliptycznością
e=b/a
-1e 1
3
Przy czym parametry parametry imożna wyrazić jako:
Stan polaryzacji fali quasi-monochromatycznej
w takim przypadku trajektoria końca wektora elektrycznego
na płaszczyźnie obserwacji może mieć charakter częściowo
uporządkowany. Mówimy wtedy o polaryzacji częściowej,
którą ilościowo opisuje parametr nazywany stopniem
polaryzacji:
0P1
gdzie IP jest natężeniem składowej wiązki całkowicie
spolaryzowanej, a I0 jest całkowitym natężeniem wiązki
4
Wektor Jonesa (tylko dla światła całkowicie
spolaryzowanego P=1)
Wprowadzając nastepujace parametry:
Definiujemy znormalizowany wektor Jonesa
I mx 2 m y 2
1
J0
I
cos
i
sin e
5
Związek pomiędzy parametrami używanymi w różnych
sposobach opisu stanu polaryzacji:
6
Zjawisko podwójnego załamania światła w
kryształach (dwójłomność)
1) W krysztale jednoosiowym istnieje fala zwyczajna, która
ma współczynnik załamania n0 nie zależy od kierunku
propagacji
2) Dla fali nadzwyczajnej współczynnik załamania n zależy
od kierunku propagacji (kąta nachylenia względem osi
optycznej)
3) Obie fale są spolaryzowane liniowe: wektor elektryczny fali
zwyczajnej drga prostopadle do płaszczyzny wyznaczonej
przez kierunek propagacji i oś optyczną. Wektor elektryczny
fali nadzwyczajnej drga w tej płaszczyźnie.
7
4) Maksymalna wartość współczynnika załamania fali
nadzwyczajnej jest oznaczana przez ne
5) Różnica współczynników załamania
no-ne
jest nazywana dwójłomnością kryształu.
8
Transformacja stanu polaryzacji w opisie
macierzowym
Transformację stanu polaryzacji przez element optyczny można
przedstawić w zapisie macierzowym
9
gdzie J1 i J2 są wektorami Jonesa padającego i wyjściowego
stanu polaryzacji, a macierz T reprezentuje właściwości
polaryzacyjne ośrodka i nazywana jest macierzą Jonesa
Macierze Jonesa dla wybranych elementów
polaryzacyjnych:
1) Idealny polaryzator liniowy o różnych kierunkach
przepuszczania
2) Polaryzator kołowy:
10
2) Płytka fazowa (opóźniająca), oś szybsza w kierunku x
Zasada działania ćwierćfalówki (/4) i półfalowki
(/2)
11
12
13
4) Macierz obrotu stanu polaryzacji
5) Macierz Jonesa w transformowanym
... zobacz całą notatkę






Komentarze użytkowników (0)