To tylko jedna z 11 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
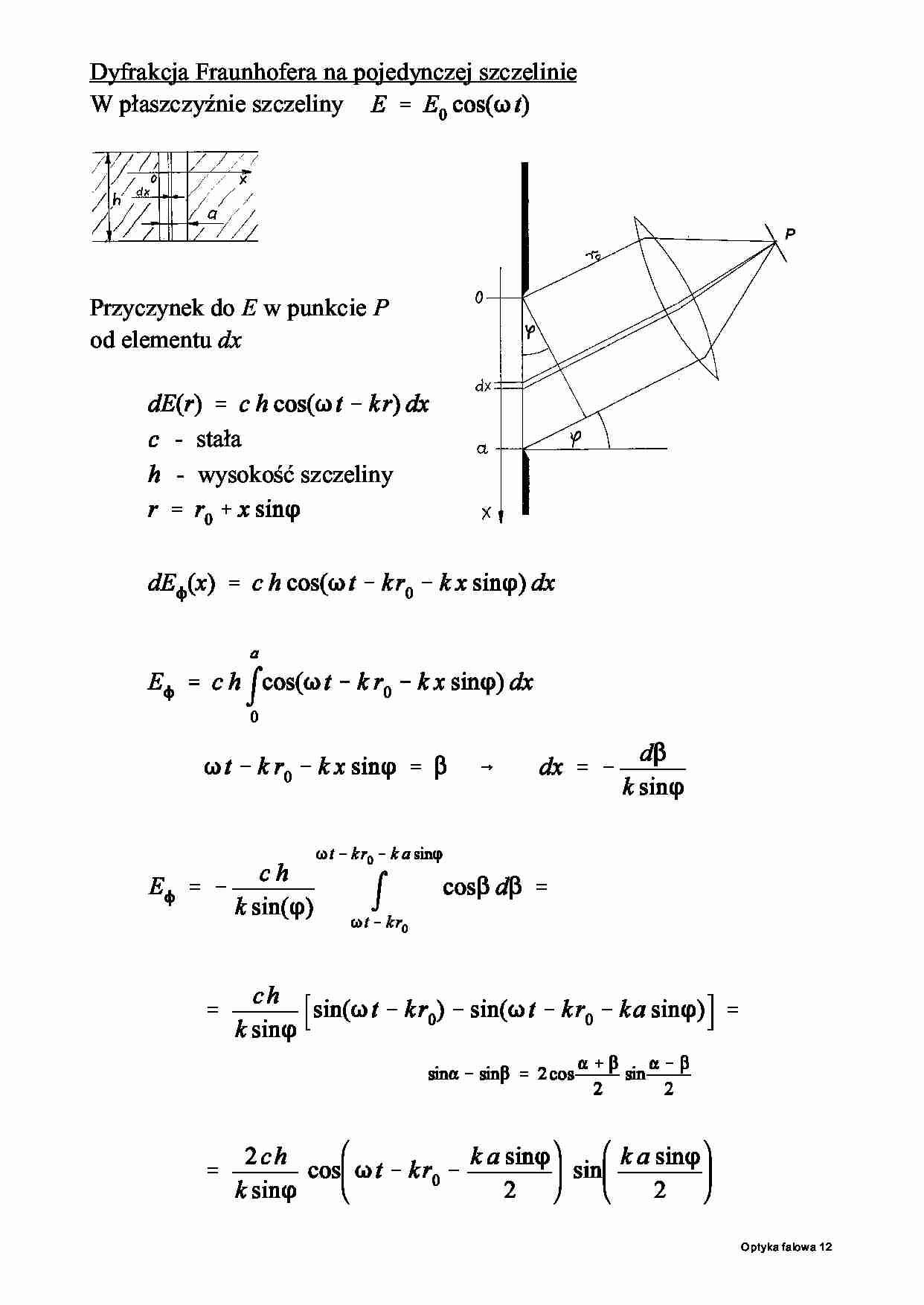


Dyfrakcja Fraunhofera na pojedynczej szczelinie
W p»aszczyïnie szczeliny
Przyczynek do E w punkcie P
od elementu dx
- sta»a
- wysokoÑ szczeliny
6
Optyka falowa 12
Natóenie
przyjmuje wartoÑ maksymaln,
, dla
, czyli dla
. Std
Optyka falowa 13
Po»oóenie minimów dyfrakcyjnych za pojedyncz szczelin
6
Optyka falowa 14
Po»oóenie maksimów dyfrakcyjnych za pojedyncz szczelin
Warunek na ekstremum
Dwie moóliwoÑci
a)
b)
6
6
- nieosigalne
6
-
odrzucamy, bo to jest warunek na minima, a
szukamy po»oóenia maksimów
6
przyblióenie tym lepsze im m
wiksze
Optyka falowa 15
Dyfrakcja Fraunhofera na otworze ko»owym
Dla prostoktnej szczeliny o wysokoÑci h
Dla otworu ko»owego o Ñrednicy D
Centralna jasna plamka - tarcza Airy’ego
Warunek dla kta , pod jakim powstaje pierwsze minimum
Optyka falowa 16
Dyfrakcja Fraunhofera na siatce dyfrakcyjnej
Siatka dyfrakcyjna - duóa liczba (N) jednakowych szczelin rozmieszczona
w sta»ych odleg»oÑciach od siebie.
Sta»a siatki
- odleg»oÑ (b) midzy Ñrodkami ssiednich szczelin.
Pole elektryczne w punkcie P jest
superpozycj pól generowanych
przez poszczególne szczeliny, ale
opóïnionych w fazie o
,
,
Dla pojedynczej szczeliny by»o
Dla N szczelin mamy wic
Optyka falowa 17
a - szerokoÑ pojedynczej szczeliny
b - dleg»oÑ midzy Ñrodkami ssiednich szczelin (sta»a siatki)
ZaleónoÑ natóenia Ñwiat»a od kta ugicia
dyfrakcyjn o N szczelinach
po przejÑciu przez siatk
- natóenie Ñwiat»a obserwowane dla
Przypadek N = 1 (pojedyncza szczelina)
6
Przypadek N = 2 (opis doÑwiadczenia Younga z iloÑciowym uwzgldnieniem
dyfrakcji)
Optyka falowa 18
W ykresy czynnika interferencyjnego i dyfrakcyjnego dla N = 2, a = 5 8 i b = 50 8
Dla
bardzo wskich szczelin
Y
Y
Podobnie jak dla interferencji Ñwiat»a z dwóch ïróde» o jednakowych
natóeniach
Optyka falowa 19
Siatka o N szczelinach
,
Minima czynnika dyfrakcyjnego gdy
,
Maksima g»ówne - maksima czynnika interferencyjnego, gdy
Y
,
m - rzd ugicia siatki
W maksimach g»ównych czynnik interferencyjny przybiera wartoÑ 1.
Maksima boczne - maksima inne nió maksima g»ówne. Midzy kaód
par maksimów g»ównych s
maksima boczne.
Minima dodatkowe- minima czynnika interferencyjnego, wystpuj wtedy
gdy
,
dla
oraz
dla
Midzy kaód par maksimów g»ównych jest
minimów.
Optyka falowa 20
ZdolnoÑ rozdzielcza siatki dyfrakcyjnej
Kryterium Rayleigha
Dwie d»ugoÑci fali moóna rozdzieli, jeóeli maksimum dyfrakcyjne
jednej z nich leóy nie blióej nió w pierwszym minimum dyfrakcyjnym
drugiej.
R - zdolnoÑ
rozdzielcza
Za»óómy, óe maksimum dyfrakcyjne dla
ktem
obserwowane jest pod
. Mamy wic
6
Za»óómy teó, óe pod tym samym ktem
obserwowane jest
pierwsze minimum dyfrakcyjne dla , czyli óe zachodzi
6
Optyka falowa 21
Y
Optyka falowa 22
... zobacz całą notatkę






Komentarze użytkowników (0)