To tylko jedna z 15 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
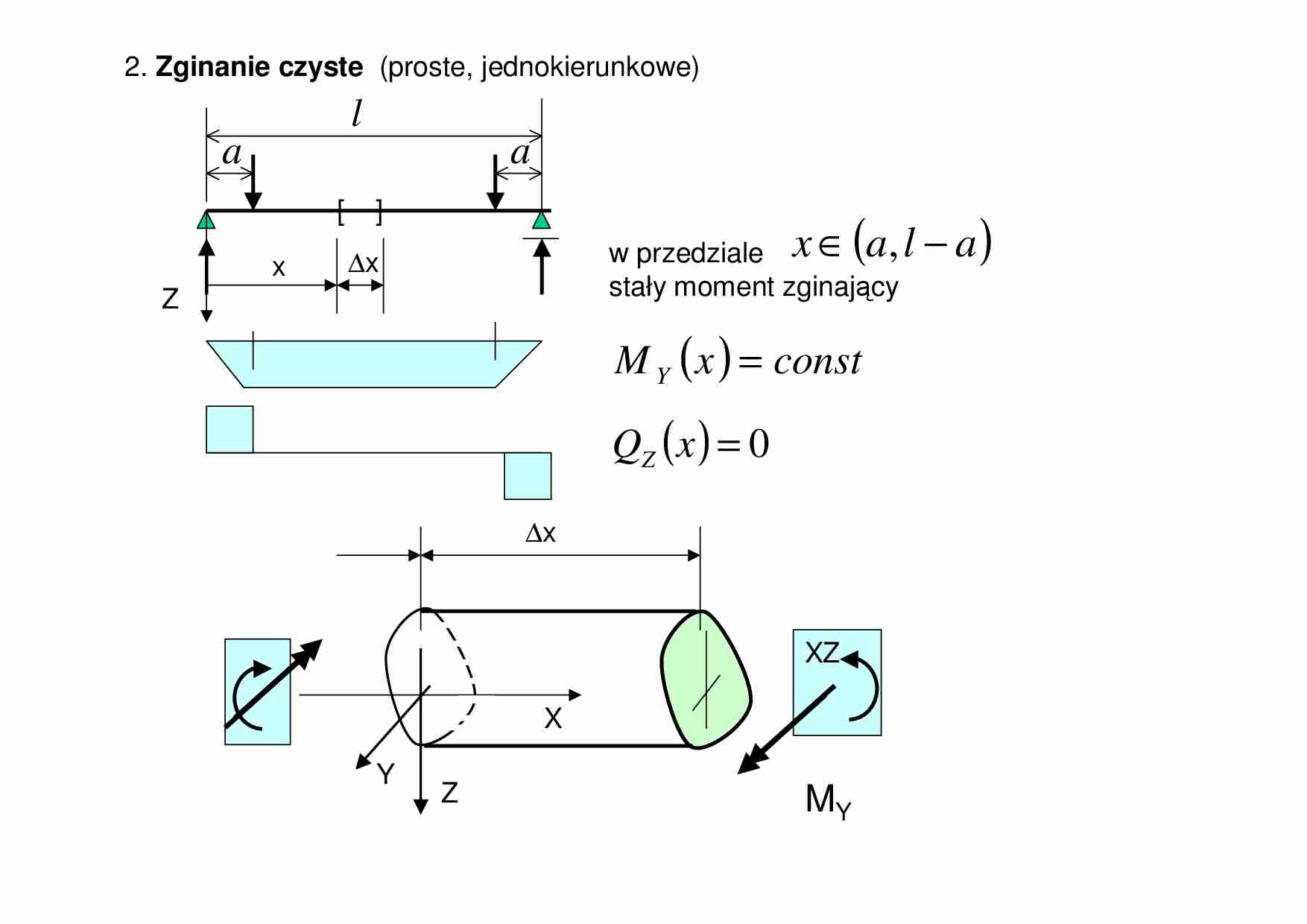


2. Zginanie czyste (proste, jednokierunkowe) M Y XZ X Y Z ∆x w przedziale stały moment zginający ( ) const x M Y = ( ) 0 = x Q Z ( ) a l a x − ∈ , x [ ] ∆x Z a a l Podstawowe zaleŜności geometryczne ZałoŜenia: 1. oś Z zaczyna się w warstwie obojętnej ( ) 2. deformacja zachodzi jedynie w płaszczyźnie XZ 0 = XX ε ( ) z z z AB AB B A l AB XX XX ⋅ = = = ∆ ∆ − ∆ + = = − = ∆ = ∆ = → ∆ → ∆ κ ε κ ρ ρ φ ρ φ ρ φ ρ ε φ ρ ρ φ φ 1 lim ' ' lim 0 0 - krzywizna - promień krzywizny ρ Z X A’ B’ A B Y M warstwa obojętna, nie ulega skróceniu/wydłuŜeniu 0 = XX ε φ ∆ l ∆ To jest jedyna postać pola odkształceń kinematycznie dopuszczalna (zasada płaskich przekrojów) Jak wyliczyć krzywiznę ? κ ( ) ( ) Y F F F XX Y YZ YZ F F F XX Z Y Y F F F XX XX XX I E dF z E dF E z dF z M D D E dF yz E dF yzE dF y M S S E dF z E dF z E dF N z E z y E z y ⋅ = = = = = ⇒ ⋅ − = − = − = − = = = ⇒ = ⋅ = = = ⋅ = = = ⋅ = = ∫ ∫ ∫ ∫ ∫ ∫ ∫ ∫ ∫ κ κ κ σ κ κ κ σ κ κ κ σ κ ε σ 2 2 0 ) ( 0 0 0 0 , , Rozkład napręŜeń: w pł. YX: Warunki równowaŜności momentów: w pł. ZX: czyli na to by zginanie w pł. ZX nie powodowało krzywizny w pł. YZ, płaszczyzny te musza być płaszczyznami głównymi przekroju Warunek równowaŜności sił w kierunku X: czyli warstwa obojętna przy zginaniu (gdzie zaczynał się nasz u.w.) przechodzi przez środek cięŜkości. Oś pręta jest osią centralną ( ) ( ) z I M z I E M E z z EI M z EI M Y Y Y Y XX Y Y XX Y Y = / / = = = σ ε κ Krzywizna: Odkształcenia: NapręŜenia: z _ + 0 Y M XX XX ε σ , strefa ściskana strefa rozciągana spody rozciągane rozkłady odkształceń i napręŜeń są liniowe, ( ) w środku cięŜkości ( ) ( ) 0 0 , 0 0 = = XX XX σ ε przy czystym zginaniu : W praktyce: Teoria czystego zginania jest teŜ słuszna w przypadku dowolnego rozkładu Dochodzi wtedy wpływ sił poprzecznych, który daje dodatkowo napręŜenia
(…)
… XX = κ Y z , σ XX = Eκ Y z
l
M
ES
1
1
2
= ∫ ε XX σ XX dV = ∫ ∫ E (κ Y z ) dF dx =
2Ω
20F
6 IY 8
7
M (x )
1
= ∫ E Y 2 ∫ z 2 dF dx =
2 0 (EI Y ) F
2
l
1 M (x )
1
= ∫ Y
dx = ∫ κ Y (x )M Y (x )dx
2 0 EI Y
20
2
l
κY
MY
l
krzywizna jest odkształceniem uogólnionym
moment zginający -napręŜeniem uogólnionym
Praca wirtualna sił wewnętrznych w pręcie zginanym w jednej płaszczyźnie gł. (XZ)
l
δW M = ∫ δκ Y ⋅ M…
… z materiału o róŜnej wytrzymałości na rozciąganie i ściskanie.
Określić jakim obciąŜeniem P moŜna ją obciąŜyć. f t = 60 MPa, f c = 80 MPa
30kN
P
−
[cm]: h = 7.5
[m]:
2
3
2
15 ⋅ 5 ⋅ 7.5 + 15 ⋅ 5 ⋅17.5 1875
=
= 12.5cm
15 ⋅ 5 + 15 ⋅ 5
150
h − = 15 + 5 − 12.5 = 7.5cm, h + = 12.5cm
eY =
h + = 12.5
15 ⋅ 53
153 ⋅ 5
2
2
I=
+ (17.5 − 12.5) ⋅ 75 +
+ (7.5 − 12.5) ⋅ 75 = 5312cm 4
12
12
I
5312
I
5312
W− =
=
= 708cm3…
…
MY moment zginający -napręŜeniem uogólnionym
Praca wirtualna sił wewnętrznych w pręcie zginanym w jednej płaszczyźnie gł. (XZ)
l
δW M = ∫ δκ Y ⋅ M Y dx
0
Zagadnienia techniczne dla zginania (przekroje z 1 osią symetrii, materiał z taką
samą wytrzymałością na ściskanie i rozciąganie np. w konstrukcjach metalowych )
MY
σG = − hG
IY
hG x
y z MY
z
hD
MY
σD = hD
IY
z max = max ( hD , hG )
MY M
σ max = z max…
… + + = 174100.0cm 4
dokładnych 12 2 2 12
82
zmax = + 1.6 = 42.6cm
2
174100.0cm 4
W= = 4088cm3 ≥ Wmin = 4057cm3
42.6cm
Przykład 4.
Belkę wykonano z materiału o róŜnej wytrzymałości na rozciąganie i ściskanie.
Określić jakim obciąŜeniem P moŜna ją obciąŜyć. f t = 60 MPa, f c = 80 MPa
30kN P
− 5
[cm]: h = 7.5
15
[m]: 2 3 2
5
15
h + = 12.5
15 ⋅ 5 ⋅ 7.5 + 15 ⋅ 5 ⋅17.5 1875
eY = = = 12.5cm
15 ⋅ 5 + 15 ⋅ 5 150
h…
… przy tym sprawdzić oznaczenia tablicowe,
oznaczenia na ogół są inne
I200 z tablic, wskaźnik wytrzymałości Wx = 214.0 cm3
x x M 30.0 kNm
σ max = = 3
=
W 214.0 cm
kNm
= 0.1402 ⋅ −6 3 = 140.2 MPa ≤ f d = 210MPa (stal St3S)
10 m
b) ok. 60% wykorzystania przekroju, dobieramy mniejszy przekrój (Typ zadania 2)
M 30 kNm /
kNm m 2
Wmin = = ⋅ = 0.143 3 ⋅
f d 210 MPa 10 kN/
= 143.0 ⋅10 −6 m 3 = 143.0cm3
I180 → Wx = 161.0cm3…
…
-koło:
πD 4
D
D
IY =
, z max =
64
2
IY
2 ⋅ πD 4 πD 3
WY =
=
=
z max
64 D
32
Przykład 1.
a) Sprawdzić napręŜenia w przekroju I200 przy zginaniu momentem M=30kNm
(Typ zadania 1)
UWAGA: korzystamy z tablic profili walcowanych,
naleŜy przy tym sprawdzić oznaczenia tablicowe,
płaszczyzna zginania
oznaczenia na ogół są inne
I200 z
x
x
tablic, wskaźnik wytrzymałości
M
Wx = 214.0 cm3
30.0 kNm
=
3
W
214.0 cm…
... zobacz całą notatkę






Komentarze użytkowników (0)