To tylko jedna z 2 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
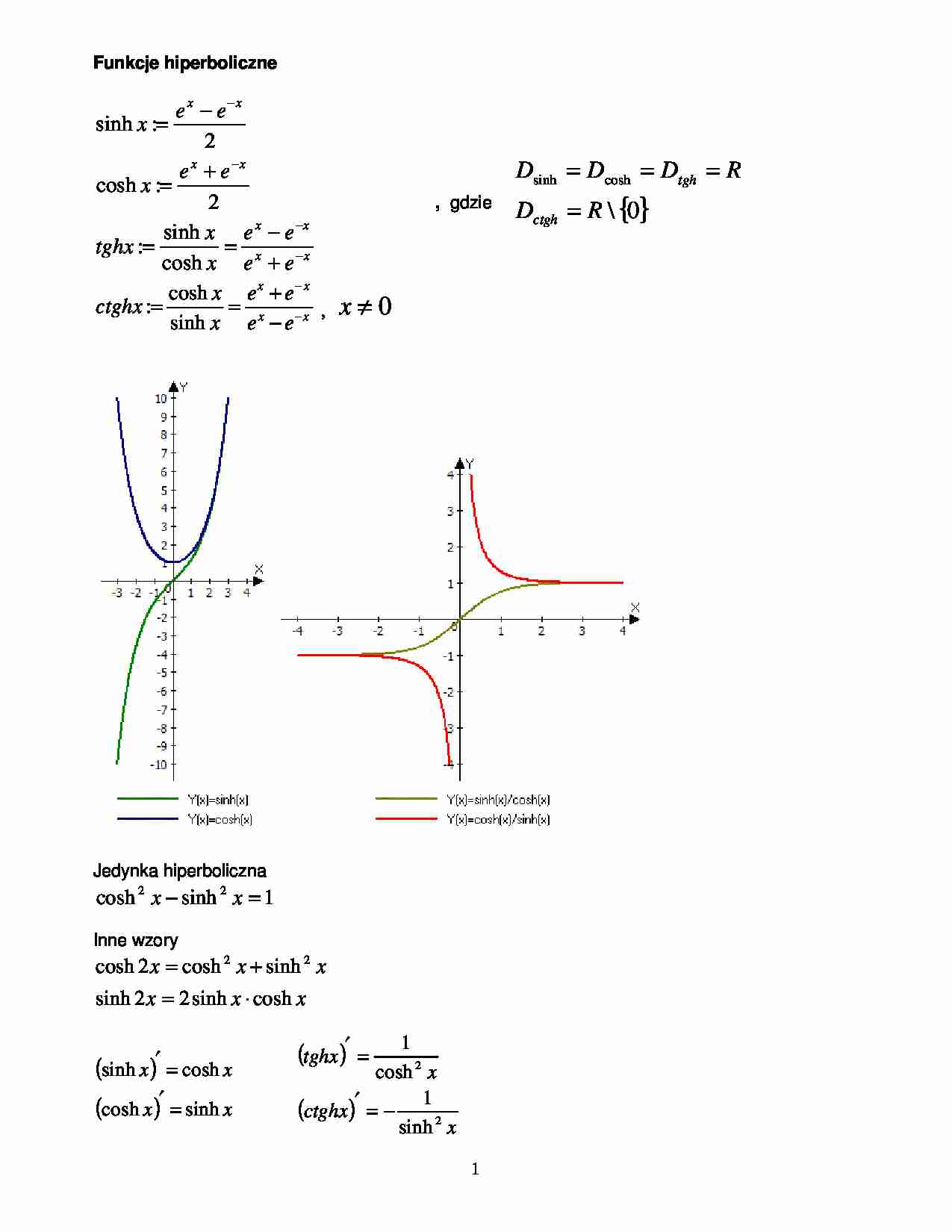

1 Funkcje hiperboliczne x x x x x x x x e e e e x x tghx e e x e e x − − − − + − = = + = − = cosh sinh : 2 : cosh 2 : sinh , gdzie { } 0 \ cosh sinh R D R D D D ctgh tgh = = = = x x x x e e e e x x ctghx − − − + = = sinh cosh : , 0 ≠ x Jedynka hiperboliczna 1 sinh cosh 2 2 = − x x Inne wzory x x x x x x cosh sinh 2 2 sinh sinh cosh 2 cosh 2 2 ⋅ = + = ( ) ( ) x x x x sinh cosh cosh sinh = ′ = ′ ( ) ( ) x ctghx x tghx 2 2 sinh 1 cosh 1 − = ′ = ′ 2 Nazwa (sinus hiperboliczny, …) wzi ła si st d, e funkcje sinh i cosh ( ) ( ) = = t b t y t a t x sinh cosh , R t ∈ które okre la hiperbol , bo ( ) ( ) 1 2 2 2 2 = − b t y a t x
... zobacz całą notatkę




Komentarze użytkowników (0)