To tylko jedna z 2 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę

Redukcja kierunków i boków w odwzorowaniu G-K
Redukcja kierunków i redukcja boków w odwzorowaniu wiernokątnym Gaussa-Krugera.
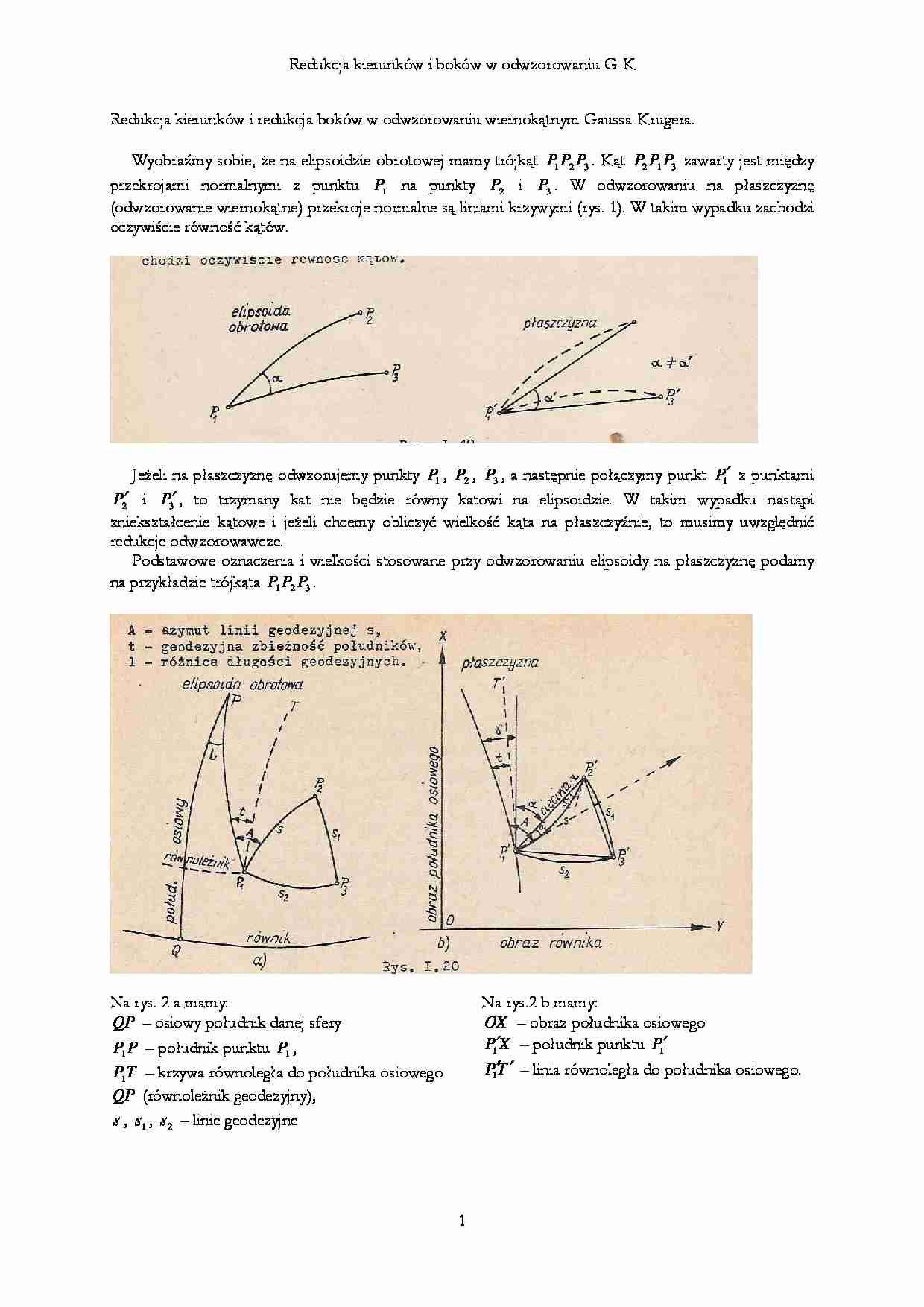
Wyobraźmy sobie, że na elipsoidzie obrotowej mamy trójkąt P1 P2 P3 . Kąt P2 P1 P3 zawarty jest między
przekrojami normalnymi z punktu P1 na punkty P2 i P3 . W odwzorowaniu na płaszczyznę
(odwzorowanie wiernokątne) przekroje normalne są liniami krzywymi (rys. 1). W takim wypadku zachodzi
oczywiście równość kątów.
Jeżeli na płaszczyznę odwzorujemy punkty P1 , P2 , P3 , a następnie połączymy punkt P1′ z punktami
P2′ i P3′ , to trzymany kat nie będzie równy katowi na elipsoidzie. W takim wypadku nastąpi
zniekształcenie kątowe i jeżeli chcemy obliczyć wielkość kąta na płaszczyźnie, to musimy uwzględnić
redukcje odwzorowawcze.
Podstawowe oznaczenia i wielkości stosowane przy odwzorowaniu elipsoidy na płaszczyznę podamy
na przykładzie trójkąta P1 P2 P3 .
Na rys.2 b mamy:
OX – obraz południka osiowego
P1′X – południk punktu P1′
P1′ ′ – linia równoległa do południka osiowego.
T
Na rys. 2 a mamy:
QP – osiowy południk danej sfery
P1 P – południk punktu P1 ,
P1T – krzywa równoległa do południka osiowego
QP (równoleżnik geodezyjny),
s , s1 , s 2 – linie geodezyjne
1
Redukcja kierunków i boków w odwzorowaniu G-K
Wskutek wiernokątności kąty między odpowiednimi liniami będą zachowane. Kąty w wierzchołkach
P1 P2 P3 trójkąta geodezyjnego są równe kątom trójkąta płaskiego P1′P2′P3′ utworzonego przez krzywe –
obrazy boków trójkąta na płaszczyźnie. Kąt między cięciwą a linią równoległą do południka osiowego
nazywa się kątem kierunkowym na płaszczyźnie i oznacza się literą α . Kąt γ nazywa się kątem zbieżności
południków na płaszczyźnie. Kąt δ (zawarty między cięciwą i obrazem linii geodezyjnej) nazywa się
redukcją kierunku. Różnica γ − t jest wielkością małą czwartego rzędu:
γ −t =
2 2 2
l η sin B cos 2 B
3
Kolejność przejścia z elipsoidy na płaszczyznę Gaussa – Krugera.
1. Przeliczenie współrzędnych B, L na współrzędne płaskie X , Y .
2. Przeliczamy azymut wyjściowej linii geodezyjnej na odpowiadający tej linii kąt kierunkowy cięciwy:
α 12 = A12 − γ 1 − δ12
α 21 = A21 − γ 2 + δ 21
γ ′′ = l ′′ sin B +
kolejne obliczenie:
1 sin B ⋅ cos 2 B
(1 + 3η 2 + 2η 4 )l ′′ 3 + ...
′′ 2
3
ρ
(x 2 − x1 )
y − y1 ρ′′
(x 2 − x1 )(2 y1 + y 2 )
ys − 2
=
2R
6 6 R S2
3. Redukujemy kąty i boki na płaszczyznę Gaussa – Krugera.
Redukcję kątowe wprowadzamy według wzoru:
′′
δ12 = ρ′′
2
S
′′
′′
δ′′ = δ13 − δ12
gdzie;
δ′′ = ρ′′
13
(x3 − x1 )
2R
ys −
2
S
y 3 − y1
(x − x )
y − y1
′′
; δ12 = ρ′′ 2 2 1 y s − 2
6
2 RS
6
Dla obszaru Polski wzór ten można uprościć, przyjmując R S (średni promień krzywizny)
odpowiadający szerokości geodezyjnej B = 52 o . Otrzymamy wówczas następujący wzór na redukcję
kierunku:
δ′′ = 0,0008439(x 2 − x1 )(2 y1 + y 2 )
gdzie x i y należy wziąć w kilometrach.
Redukcję boków wyznaczamy ze wzoru:
{
(
2
d = D 1 + 0,0000000040 9 ⋅ y12 + y1 y 2 + y 2
gdzie y należy wziąć w kilometrach.
2
)}
... zobacz całą notatkę




Komentarze użytkowników (0)