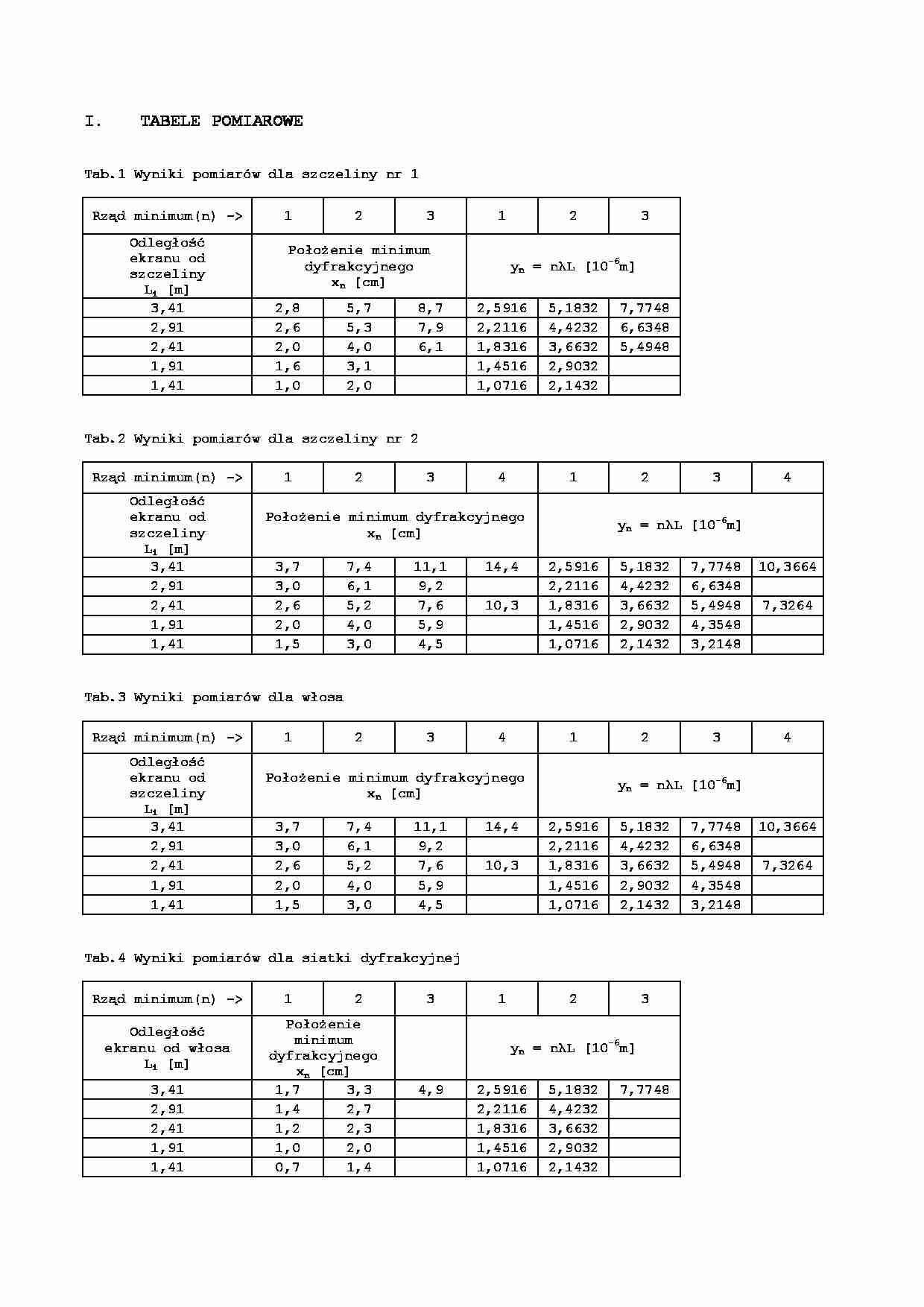
TABELE POMIAROWE Tab.1 Wyniki pomiarów dla szczeliny nr 1 Rząd minimum(n) - 1 2 3 1 2 3 Odległość ekranu od szczeliny L i [m] Położenie minimum dyfrakcyjnego x n [cm] y n = nλL [10 -6 m] 3,41 2,8 5,7 8,7 2,5916 5,1832 7,7748 2,91 2,6 5,3 7,9 2,2116 4,4232 6,6348 2,41 2,0 4,0 6,1 1,8316 3,6632 5,4948 1,91 1,6 3,1 1,4516 2,9032 1,41 1,0 2,0 1,0716 2,1432 Tab.2 Wyniki pomiarów dla szczeliny nr 2 Rząd minimum(n) - 1 2 3 4 1 2 3 4 Odległość ekranu od szczeliny L i [m] Położenie minimum dyfrakcyjnego x n [cm] y n = nλL [10 -6 m] 3,41 3,7 7,4 11,1 14,4 2,5916 5,1832 7,7748 10,3664 2,91 3,0 6,1 9,2 2,2116 4,4232 6,6348 2,41 2,6 5,2 7,6 10,3 1,8316 3,6632 5,4948 7,3264 1,91 2,0 4,0 5,9 1,4516 2,9032 4,3548 1,41 1,5 3,0 4,5 1,0716 2,1432 3,2148 Tab.3 Wyniki pomiarów dla włosa Rząd minimum(n) - 1 2 3 4 1 2 3 4 Odległość ekranu od szczeliny L i [m] Położenie minimum dyfrakcyjnego x n [cm] y n = nλL [10 -6 m] 3,41 3,7 7,4 11,1 14,4 2,5916 5,1832 7,7748 10,3664 2,91 3,0 6,1 9,2 2,2116 4,4232 6,6348 2,41 2,6 5,2 7,6 10,3 1,8316 3,6632 5,4948 7,3264 1,91 2,0
(…)
… siatki dyfrakcyjnej:
Tab.10 Ostateczne wyniki wyznaczonych parametrów siatki dyfrakcyjnej Stała siatki dyfrakcyjnej d
6,052±0,062 μm
Liczba rys na milimetr
165 rys/mm
Liczbę rys na milimetr, zapisaną w powyższej tabeli, wyznaczono ze wzoru:
OCENA NIEPEWNOŚCI POMIAROWYCH
Niepewności standardowe współczynników kierunkowych prostych regresji wyznaczono przy pomocy wbudowanej funkcji REGLINP() arkusza kalkulacyjnego Microsoft Excel. Otrzymane wartości niepewności zapisano w odpowiednich kolumnach tabel 5, 6, 7, 9.
Niepewność maksymalną szerokości szczelin, grubości włosa oraz stałej siatki dyfrakcyjnej wyznaczono mnożąc niepewność standardową przez pierwiastek z trzech. Przy czym, ponieważ przeprowadzono więcej niż jeden pomiar każdej z szukanych wielkości, otrzymując różne wartości niepewności standardowych…
…
Odległość ekranu od szczeliny Li [m]
Położenie minimum dyfrakcyjnego xn [cm]
yn = nλL [10-6m]
3,41
3,7
7,4
11,1
14,4
2,5916
5,1832
7,7748
10,3664
2,91
3,0
6,1
9,2
2,2116
4,4232
6,6348
2,41
2,6
5,2
7,6
10,3
1,8316
3,6632
5,4948
7,3264
1,91
2,0
4,0
5,9
1,4516
2,9032
4,3548
1,41
1,5
3,0
4,5
1,0716
2,1432
3,2148
Tab.4 Wyniki pomiarów dla siatki dyfrakcyjnej
Rząd minimum(n) ->
1
2
3
1
2
3
Odległość ekranu…
…)
n - rząd minimum dyfrakcyjnego
λ - długość fali światła, λ=760nm
L - odległość szczeliny (włosa) od ekranu
xn - położenie n-tego minimum dyfrakcyjnego (odległość od centrum obrazu)
Powyższy wzór możemy przekształcić do postaci:
Powyższą zależność możemy potraktować jako wzór funkcji liniowej:
yn = axn gdzie:
yn = nλL
xn = xn
a = d
Powyższą zależność liniową dla każdej z badanych szczelin oraz włosa…
… standardowych wyznaczono przy pomocy wbudowanej funkcji REGLINP() arkusza kalkulacyjnego Microsoft Excel. Otrzymane wartości współczynników kierunkowych, będące zarazem szerokościami szczelin (grubością włosa), zamieszczono w poniższej tabeli:
Tab.5 Szerokość szczeliny nr 1
Lp. pomiaru
(numer rzędu minimum dyfrakcyjnego odpowiadającego danemu pomiarowi)
Szerokość szczeliny
d [μm]
Niepewność standardowa
u(d…
… pokazało przydatność zjawiska dyfrakcji przy pomiarach wielkości obiektów mikroskopijnych rozmiarów. Byliśmy w stanie zmierzyć wielkości rzędu kilku mikrometrów z bardzo wysoką dokładnością.
…
… przedstawiono na wykresach załączonych do niniejszego sprawozdania, oddzielnie dla każdego rzędu dyfrakcji, traktowanego jako stały parametr w powyższym równaniu.
Wyznaczono współczynniki kierunkowe prostych regresji, odpowiednio dla każdego z wykresów, metodą najmniejszych kwadratów, tj. ze wzoru:
gdzie:
xi - położenie minimum dyfrakcyjnego
yi = nλLi
Wartości współczynników kierunkowych oraz ich niepewności…
... zobacz całą notatkę


Komentarze użytkowników (0)