To tylko jedna z 11 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
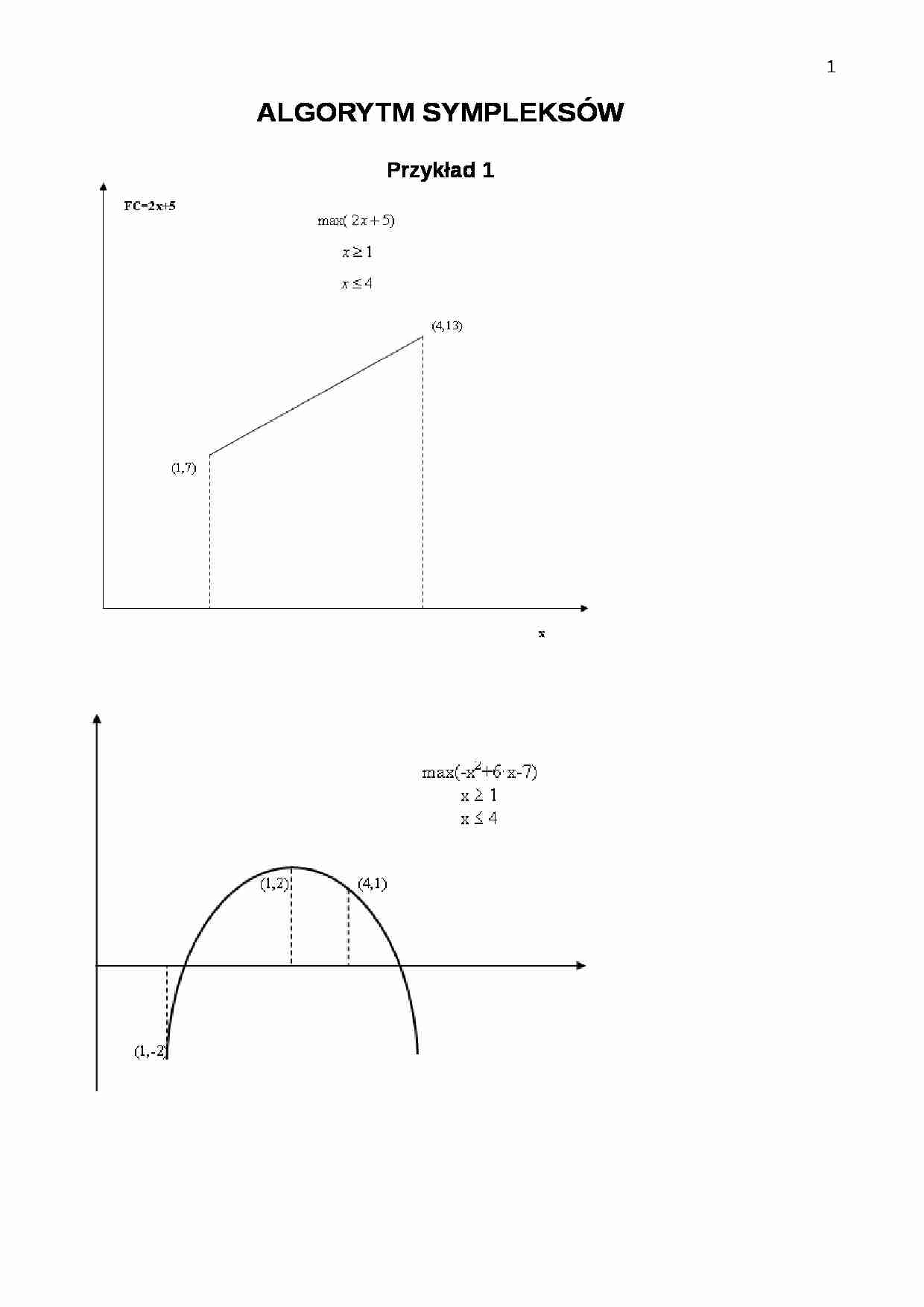


ALGORYTM SYMPLEKSÓW Przykład 1 Przykład 2 Drukarnia może wydawać ksiązki A i B, których cena wynosi odpowiednio 100 zł i 80 zł. Na książkę A zużywa się 1 kg farby i 3 kg papieru, zaś na B odpowiednio 0,5 i 4 kg. Drukarnia dysponuje 100 kg farby i 500 kg papieru. Ile książek A i B powinna wydrukować.
Wartość funkcji celu w wierzchołkach:
Fc(0,0)=0
Fc(100,0)=10 000
Fc(0,125)=10 000
Fc(60,80)=12 400 Definicje i twierdzenia : • Sympleksem jest wielościan wypukły rozpięty na n +1 wierzchołkach w przestrzeni R n • Można udowodnić, że rozwiązaniem ZPL jest jeden z wierzchołków wielościanu rozpiętego na ograniczeniach
• Metoda sympleksów polega na wyznaczaniu kolejnych wierzchołków i sprawdzaniu, czy uzyskano rozwiązanie optymalne
Macierzą bazową B układu równań A ⋅ x = b nazywamy kwadratową macierz o wymiarze m x m utworzoną z liniowo niezależnych kolumn macierzy A .
Rozwiązaniem bazowym B układu równań (6) nazywamy wektor x B = B -1 · b .
Rozwiązanie bazowe x B jest dopuszczalne, jeżeli x B ≥0.
Rozwiązanie bazowe x B jest niezdegenerowane, jeżeli x B 0.
Zmienne wchodzące w skład x B nazywamy zmiennymi bazowymi .
Pozostałe zmienne, zwane niebazowymi, tworzą wektor x P . Zmienne niebaz o we mają wartości równe 0. Rozwiązaniem optymalnym zadania programowania liniowego nazywamy rozwiązanie dopuszczalne maksymalizujące funkcję celu.
Zastosowanie algorytmu sympleksów (simpleksów) wymaga przedstawienia m e tod: 1. Znajdowania startowego dopuszczalnego rozwiązania bazowego 2. Sprawdzenia optymalności dopuszczalnego rozwiązania bazowego 3. Wyznaczenia kolejnego dopuszczalnego rozwiązania bazowego, tak aby przybliżać się do ekstremum
max c T ⋅ x n - liczba zmiennych, m - liczba ograniczeń
A ⋅ x = b x≥0
1. Początkowe dopuszczalne rozwiązanie bazowe W macierzy A odszukujemy m liniowo niezależnych jednostkowych kolumn, które wyodrębniamy i oznaczamy jako B . Kolumny pozostałe oznaczamy jako P . Kolumny macierzy B odpowiadają zmiennym bazowym , natomiast kolumny macierzy P odpowiadają zmiennym niebazowym . Niech macierz A′ =[ B P ] zostanie utworzona na podstawie macierzy A w wyniku przestawienia jej kolumn tak, aby na początku znalazły się kolumny odpowiadające zmiennym bazowym.
(…)
…] zostanie utworzona na podstawie macierzy A w wyniku przestawienia jej kolumn tak, aby na początku znalazły się kolumny odpowiadające zmiennym bazowym.
Jeżeli w macierzy A nie można znaleźć macierzy jednostkowej o wymiarze m x m, należy wprowadzić zmienne sztuczne, tak aby:
A⋅x+I⋅xsz = b przy czym x≥0 i xsz ≥0
Aby zmienne sztuczne w rozwiązaniu optymalnym miały wartości zerowe stosuje się metodę kar…
... zobacz całą notatkę






Komentarze użytkowników (0)