To tylko jedna z 2 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
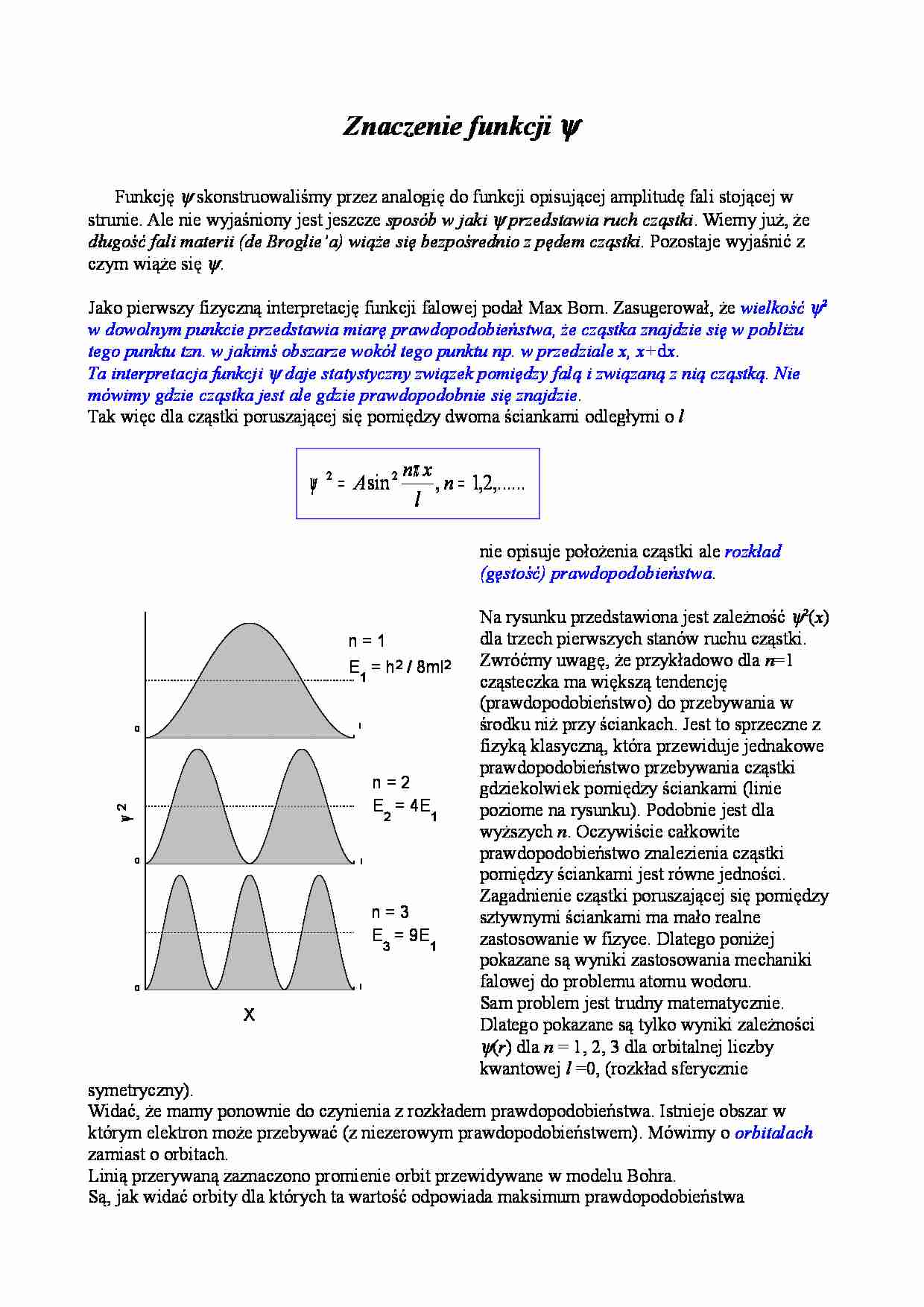

Znaczenie funkcji ψ Funkcję ψ skonstruowaliśmy przez analogię do funkcji opisującej amplitudę fali stojącej w strunie. Ale nie wyjaśniony jest jeszcze sposób w jaki ψ przedstawia ruch cząstki . Wiemy już, że długość fali materii (de Broglie’a) wiąże się bezpośrednio z pędem cząstki . Pozostaje wyjaśnić z czym wiąże się ψ. Jako pierwszy fizyczną interpretację funkcji falowej podał Max Born. Zasugerował, że wielkość ψ 2 w dowolnym punkcie przedstawia miarę prawdopodobieństwa, że cząstka znajdzie się w pobliżu tego punktu tzn. w jakimś obszarze wokół tego punktu np. w przedziale x, x+ d x . Ta interpretacja funkcji ψ daje statystyczny związek pomiędzy falą i związaną z nią cząstką. Nie mówimy gdzie cząstka jest ale gdzie prawdopodobnie się znajdzie . Tak więc dla cząstki poruszającej się pomiędzy dwoma ściankami odległymi o l ,. . . 2 , 1 , sin2 2 = = n l x n A π ψ nie opisuje położenia cząstki ale rozkład (gęstość) prawdopodobieństwa . Na rysunku przedstawiona jest zależność ψ2( x ) dla trzech pierwszych stanów ruchu cząstki. Zwróćmy uwagę, że przykładowo dla n =1 cząsteczka ma większą tendencję (prawdopodobieństwo) do przebywania w środku niż przy ściankach. Jest to sprzeczne z fizyką klasyczną, która przewiduje jednakowe prawdopodobieństwo przebywania cząstki gdziekolwiek pomiędzy ściankami (linie poziome na rysunku). Podobnie jest dla wyższych n . Oczywiście całkowite prawdopodobieństwo znalezienia cząstki pomiędzy ściankami jest równe jedności. Zagadnienie cząstki poruszającej się pomiędzy sztywnymi ściankami ma mało realne zastosowanie w fizyce. Dlatego poniżej pokazane są wyniki zastosowania mechaniki falowej do problemu atomu wodoru. Sam problem jest trudny matematycznie. Dlatego pokazane są tylko wyniki zależności ψ( r ) dla n = 1, 2, 3 dla orbitalnej liczby kwantowej l =0, (rozkład sferycznie symetryczny). Widać, że mamy ponownie do czynienia z rozkładem prawdopodobieństwa. Istnieje obszar w którym elektron może przebywać (z niezerowym prawdopodobieństwem). Mówimy o orbitalach zamiast o orbitach. Linią przerywaną zaznaczono promienie orbit przewidywane w modelu Bohra. Są, jak widać orbity dla których ta wartość odpowiada maksimum prawdopodobieństwa ψ 2 0 l n = 2 E 2 = 4E 1 X 0 l n = 3 E 3 = 9E 1 l 0 n = 1 E 1 = h2 / 8ml2 znalezienia elektronu. n =1 0 5 10 15 20 25 r/r Bohra n = 3 n = 2 ψ (r )2 Document Outline Znaczenie funkcji
... zobacz całą notatkę




Komentarze użytkowników (0)