To tylko jedna z 10 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę

4.3. Przekształcenia automatów skończonych
Konstrukcja automatu skończonego (niedeterministycznego) na podstawie wyrażenia
regularnego (algorytm Thompsona).
Wejście: wyrażenie regularne r nad alfabetem T
Wyjście : automat skończony akceptujący język L(r) (język opisany wyrażeniem
regularnym r)
Metoda: wyodrębnić z wyrażenia regularnego r elementy podstawowe. Dla elementów
podstawowych skonstruować odpowiadające im automaty, a następnie połączyć je według
poniższych zasad:
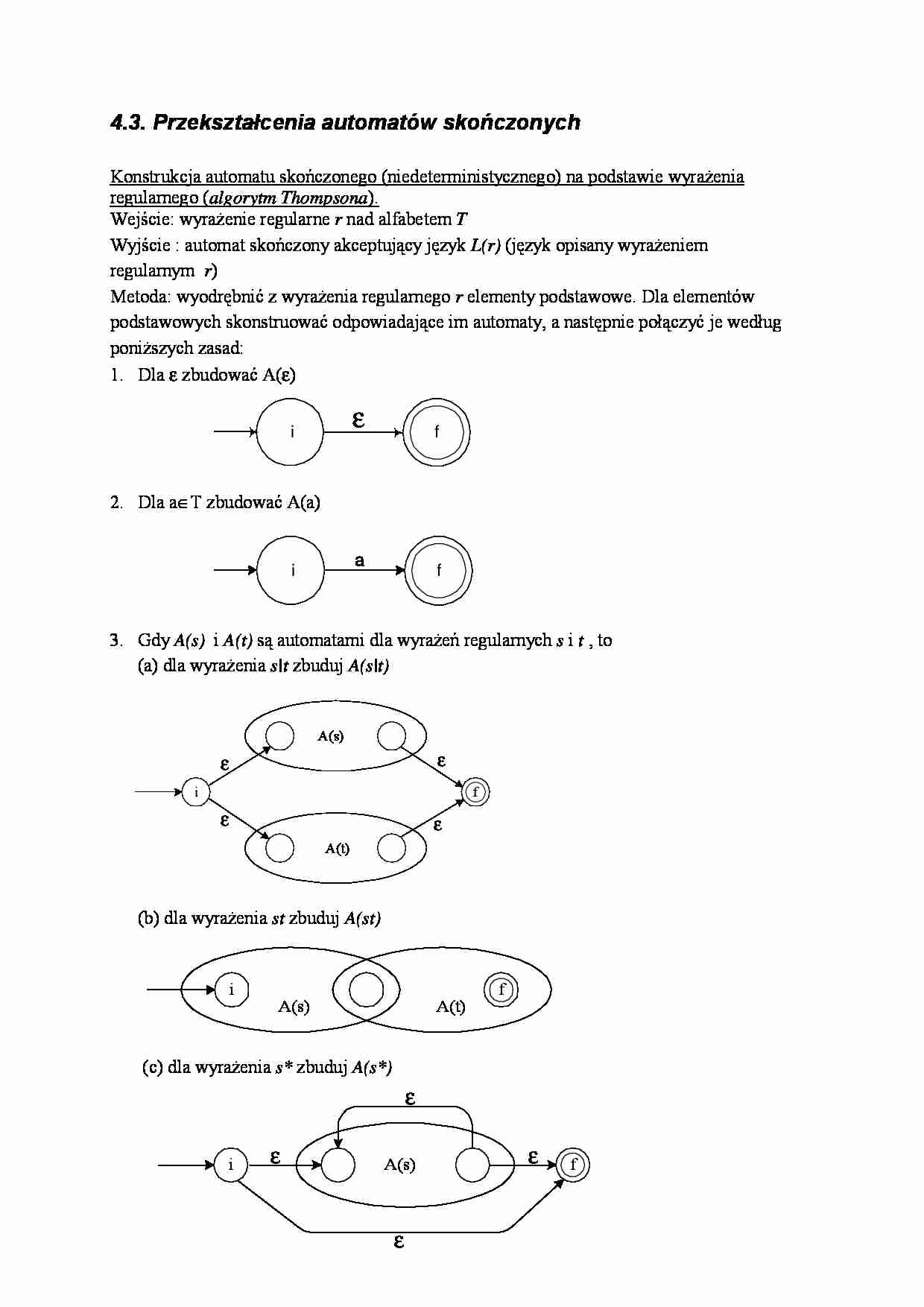
1. Dla ε zbudować A(ε)
ε
i
3
f
2. Dla a∈T zbudować A(a)
a
i
3
f
3. Gdy A(s) i A(t) są automatami dla wyrażeń regularnych s i t , to
(a) dla wyrażenia s|t zbuduj A(s|t)
A(s)
ε
ε
i
f
ε
ε
A(t)
(b) dla wyrażenia st zbuduj A(st)
i
A(s)
A(t)
f
(c) dla wyrażenia s* zbuduj A(s*)
ε
i
ε
A(s)
ε
ε
f
(d) dla wyrażenia (s) wykorzystaj A(s) bez zmian
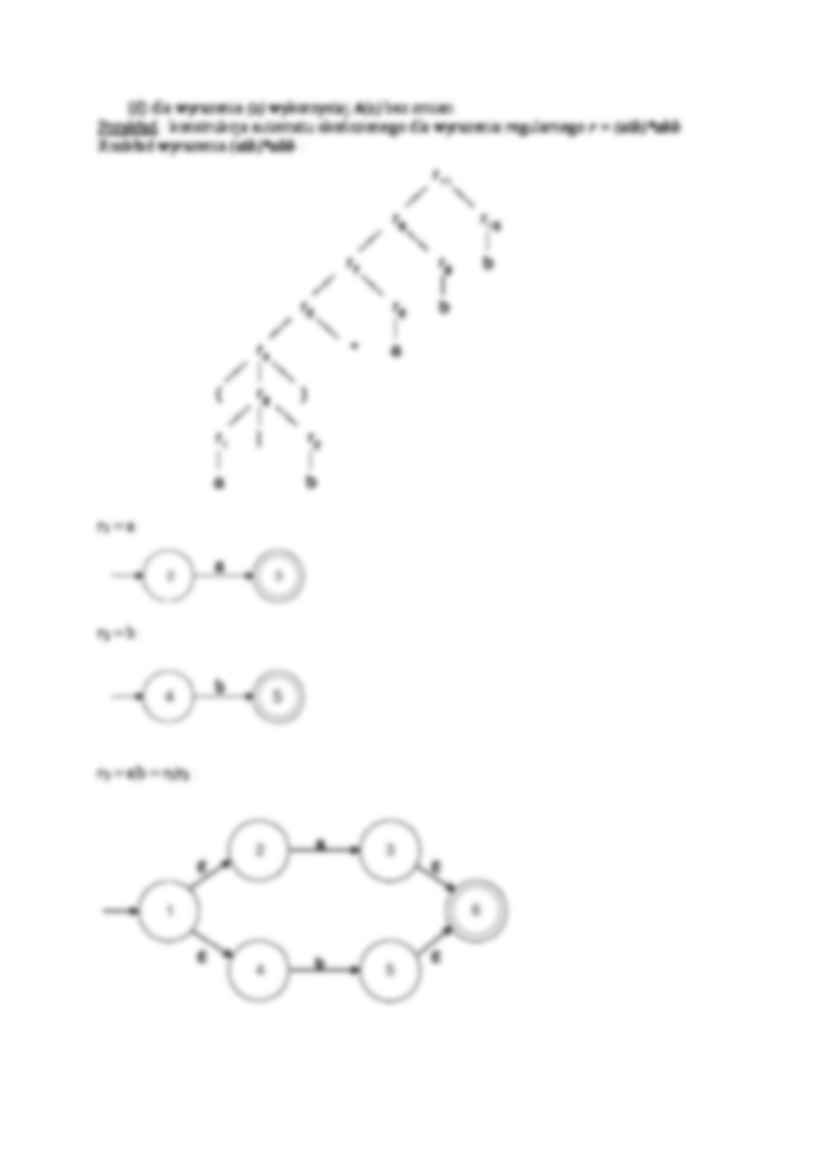
Przykład : konstrukcja automatu skończonego dla wyrażenia regularnego r = (a|b)*abb
Rozkład wyrażenia (a|b)*abb :
r11
r9
r7
r5
(
r1
*
r3
|
r8
r6
r4
r10
b
b
a
)
r2
a
b
r1 = a:
a
2
3
r2 = b:
b
4
3
5
r3 = a|b = r1|r2 :
ε
2
a
3
ε
6
3
1
ε
4
b
5
ε
r4 = (r3)
r5 = r4* :
ε
ε
ε
0
a
2
3
ε
1
ε
6
ε
b
4
5
7
3
ε
ε
r6 = a ; r8 = b ; r9 = b - konstrukcje identyczne jak dla r1 i r2
rx = abb :
a
7'
b
8
b
9
10
3
r= r5rx = (a|b)*abb
Więc ostatecznie otrzymujemy:
ε
0
ε
ε
2
a
3
ε
6
1
ε
4
b
ε
5
ε
7
a
8
b
9
b
3
10
ε
(a|b)*abb
Konstrukcja automatu deterministycznego na podstawie automatu niedeterministycznego
Dla każdego automatu skończonego istnieje deterministyczny automat skończony akceptujący
ten sam język.
Dla q∈Q definiuje się zbiór ε-CLOSURE(q) zawierający te stany r∈Q, do których można
dojść z q przechodząc tylko przez ε-przejścia, przy czym również q ∈ ε-CLOSURE(q).
Dla S⊆Q definiuje się zbiór ε-CLOSURE(S) zawierający te stany r∈Q, do których można
dojść ze stanów S przechodząc tylko przez ε-przejścia, przy czym również
S ⊆ ε-CLOSURE(S).
Dla S⊆Q, dla a∈T rozszerza się definicję funkcji przejścia:
δ(S,a) = { r∈Q | r∈δ(s,a), s∈S }
Istota algorytmu:
Wejście: A= - automat skończony niedeterministyczny
Wyjście: A’= - automat skończony deterministyczny (bez ε-przejść)
Metoda: Q⊇S ! r ∈ Q’
podzbiór zbioru stanów
automatu niederminist.
pojedynczy stan automatu
determnistycznego
r0 := ε-CLOSURE({q0});
r0 - nieoznaczony; /* r0 – stan początkowy A’ */
/* r0 – równocześnie podzbiór zbioru stanów Q automatu A */
Q’ := {r0};
while ∃ X∈Q’ and X – nieoznaczony do
/* X = {q1,...,qn} ⊆ Q*/
begin
oznacz X;
for każde a∈T do
begin
U := {q∈Q | q∈δ(s,a) ∧ s∈X } /* U = δ(X,a) */
Y := ε-CLOSURE(U) ;
if Y∉Q’ then
begin
Q’ := Q’ ∪ {Y};
/* dołączenie Y do Q’
Y – nieoznaczony
jako nieoznaczonego */
end;
δ’(X,a) := Y;
/* ustalenie funkcji przejścia automatu A’ */
end;
end;
F’ := { r ∈ Q’ | r ∩ F ≠ ∅ } /* tutaj r traktowane jako (r⊂Q) podzbiór stanów automatu A */
Przykład:
ε
0
ε
ε
2
a
3
ε
6
1
ε
4
b
ε
5
ε
7
a
b
8
9
ε
... zobacz całą notatkę






Komentarze użytkowników (0)